The classical author Epictetus (ca 50–ca 138 AD) once said, ‘The materials of action are variable, but the use we make of them should be constant’. How wise. When we build a house, we only require a certain number of We give the name ‘compound unit’ to several units written together. We leave a space between each constituent unit when we write such a compound unit. building materials: say, bricks, tubes and window panes. The quantity surveyor in charge of the building project decides which materials are needed, and writes a quantity beside each on his order form: 10 000 bricks, 20 window panes, etc. Similarly, when we have a velocity, we have the units of ‘m’ and ‘s−1’, and then quantify it, saying something like, ‘The man ran fast, covering a distance of 10 metres per second’. By this means, any parameter is defined both qualitatively (in terms of its units) and quantitatively (in terms of a number). With symbols, we would write v = 10 m s−1.

We sometimes call it a ‘phrase’. Because some numbers are huge ‘Giga’ comes from the Latin gigas, meaning ‘giant’ or ‘huge’. We also get the everyday words ‘giant’ and ‘gigantic’ from this root. In physical chemistry, a ‘factor’ is a number by which we multiply the numerical value of a variable. Factors are usually employed with a shorthand notation. and others tiny, the SI system allows us a simple and convenient shorthand. We do not need to write out all the zeros, saying the velocity of light c is 300 000 000 m s−1: we can write it as c = 3 × 108 m s−1 or as 0.3 Gm s−1, where the capital ‘G’ is a shorthand for ‘giga’, or 1 000 000 000. The symbol G (for giga) in this context is called a ‘factor’. In effect, we are saying 300 000 000 m s−1 = 0.3 Gm s−1. The standard factors are listed on pp. xxviii–xxxi. Most people find that writing 300 000 000 m s−1 is a bit long winded. Some people do not like writing simple factors such as G for giga, and prefer so-called scientific notation. In this style, we write a number followed by a factor expressed as ten raised to an appropriate power. The number above would be 3.0 × 108 m s−1.

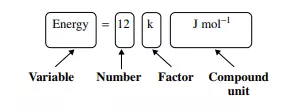
Reasoning Variable – in simple mathematical ‘phrases’ such as this, we almost always write the variable on the left. A variable is a quantity whose value can be altered. Number – the easy part! It will be made up of numbers 1, 2, 3,…, 0. Factor – if we need a factor, it will always be written between the number and the units (compound or single). A comprehensive list of the simple factors is given on pp. xxviii–xxxi. Units – the units are always written on the right of a phrase such as this. There are two units here, joules (J) and moles (as ‘mol−1 ’, in this case). We should leave a space between them.