The air around a hot radiator soon acquires heat. We explain this observation from the ‘minus oneth law of thermodynamics’ (see Section 1.1), since heat travels from hot to cold. The density of a gas depends quite strongly on its temperature, so hot air has a smaller density than does cold air; colder air is more dense than hot air. From everyday experience, we know that something is dense if it tries to drop, which is why a stone drops to the bottom of a pond and a coin sinks to the bottom of a pan of water.
This relative motion occurs because both the stone and the coin have higher densities than does water, so they drop. Similarly, we are more dense than air and will drop if we fall off a roof. Just like the coin in water, cold air sinks because it is denser than warmer air. We sometimes see this situation stated as warm air ‘displaces’ the cold air, which subsequently takes its place.
Alternatively, we say ‘warm air rises’, which explains why we place our clothes above a radiator to dry them, rather than below it. Light entering the room above the radiator passes through these pockets of warm air as they rise through colder air, and therefore passes through regions of different density. The rays of light bend in transit as they pass from region to region, much in the same way as light twists when it passes through a glass of water.
We say the light is refracted. The eye responds to light, and interprets these refractions and twists as different intensities. So we see swirling eddy (or ‘convective’) patterns above a radiator because the density of air is a function of temperature. If all the air had the same temperature, then no such difference in density would exist, and hence we would see no refraction and no eddy currents – which is the case in the summer when the radiator is switched off. Then again, we can sometimes see a ‘heat haze’ above a hot road, which is caused by exactly the same phenomenon.
The effect of pressure on gas volume:
Boyle’s law It is easy to buy canisters of gas of many sizes, e.g. as fuel when we wish to camp in the country, or for a portable welding kit. The gas will be n-butane if the gas is for heating purposes, but might be oxygen or acetylene if the gas is to achieve the higher temperatures needed for welding. Typically, the components within the can are gaseous at most temperatures.
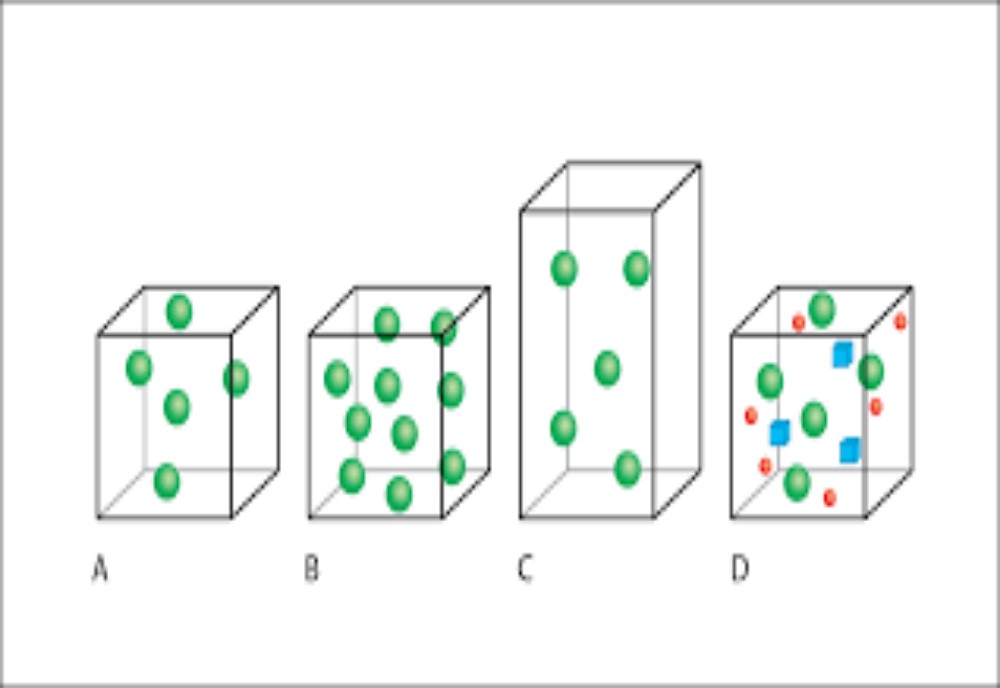
The typical volume of an aerosol can is about 0.3 dm3 (3 × 10−4 m3), so it could contain very little gas if stored at normal pressure. But if we purchase a canister of gas and release its entire contents at once, the gas would occupy a volume similar that of an entire living room. To ensure the (small) can contains this (large) Care: a small p indicates pressure, yet a big P is the symbol for the element phosphorus. Similarly, a big V indicates volume and a small v is the symbol for velocity. amount of gas, we pressurize it to increase its capacity.
We see how volume and pressure are interrelated in a reciprocal way: the volume decreases as the pressure increases. Robert Boyle was the first to formulate a relationship between p and V . Boyle was a contemporary of the greatest scientist the world has ever seen, the 17th-century physicist Sir Isaac Newton. Boyle’s law was discovered in 1660, and states
where the numerical value of the constant on the right-hand side of the equation depends on both the identity and amount of the gas, as well as its temperature T . Figure 1.6 shows a graph of pressure p (as y) against volume V An ‘isotherm’ is a line on a graph representing values of a variable obtained at constant temperature. (as x) for 1 mol of neon gas. There are several curves, each representing data obtained at a different temperature. The temperature per curve was constant, so we call each curve an isotherm. The word isotherm has two Greek roots: iso means ‘same’ and thermo means temperature or energy. An isotherm therefore means at the same energy. The actual shape of the curves in Figure 1.6 are those of reciprocals. We can prove this mathematical form if we divide both sides of Equation (1.9) by V , which yields.