Because most shear-thinning fluids, particularly polymer solutions and flocculated suspensions, have high apparent viscosities, even relatively coarse particles may have velocities in the creeping-flow of Stokes’ law regime. CHHABRA(35,36) has proposed that both theoretical and experimental results for the drag force F on an isolated spherical particle of diameter d moving at a velocity u may be expressed as a modified form of Stokes’ law:

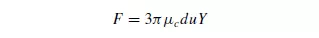
where the apparent viscosity μc is evaluated at a characteristic shear rate u/d, and Y is a correction factor which is a function of the rheological properties of the fluid. The best available theoretical estimates values of Y for power-law fluids are given in Table 3.9.

Several expressions of varying forms and complexity have been proposed(35,36) for the prediction of the drag on a sphere moving through a power-law fluid. These are based on a combination of numerical solutions of the equations of motion and extensive experimental results. In the absence of wall effects, dimensional analysis yields the following functional  relationship between the variables for the interaction between a single isolated particleand a fluid:

where CD and C_D are drag coefficients defined by equation 3.4, n is the power-law index and Re_ n is the particle Reynolds number given by:

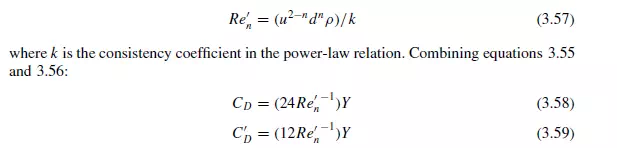
From Table 3.9 it is seen that, depending on the value of n, the drag on a sphere in a power-law fluid may be up to 46 per cent higher than that in a Newtonian fluid at the

same particle Reynolds number. Practical measurements lie in the range 1 < Y < 1.8, with considerable divergences between the results of the various workers. In view of the general uncertainty concerning the value of Y , it may be noted that the unmodified Stokes’ law expression gives a acceptable first approximation. The terminal settling velocity u0 of a particle in the gravitational field is then given by equating the buoyant weight of the particle to the drag force to give:

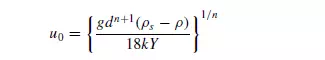
where (ρs − ρ) is the density difference between the particle and the fluid. From equation 3.59, it is readily seen that in a shear-thinning fluid (n < 1) the terminal

velocity is more strongly dependent on d, g and ρs − ρ than in a Newtonian fluid and a small change in any of these variables produces a larger change in u0.

Outside the creeping flow regime, experimental results for drag on spheres in powerlaw fluids have been presented by TRIPATHI et al.(37) and GRAHAM(38) for values of Re_N up to 100, and these are reasonably well correlated by the following expressions with an average error of about 10 per cent:

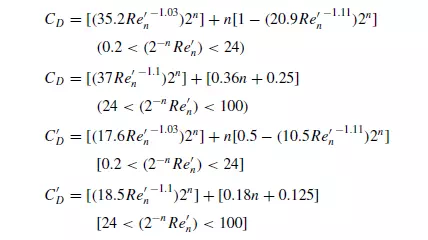
It may be noted that these two equations do not reduce exactly to the relation for a Newtonian fluid (n = 1). Extensive comparisons of predictions and experimental results for drag on spheres suggest that the influence of non-Newtonian characteristics progressively diminishes as the value of the Reynolds number increases, with inertial effects then becoming dominant, and the standard curve for Newtonian fluids may be used with little error. Experimentally determined values of the drag coefficient for power-law fluids (1 < Re _n < 1000; 0.4 < n < 1) are within 30 per cent of those given by the standard drag curve(37,38). While equations 3.62a and 3.62b are convenient for estimating the value of the drag coefficient, they need to be re-arranged in order to enable the settling velocity u0 of a sphere of given diameter and density to be calculated, since both CD(C_D) and Re_n are functions of the unknown settling velocity. By analogy with the procedure used for Newtonian fluids (equation 3.36), the dimensionless Galileo number Gan which is independent of u0 may be defined by:

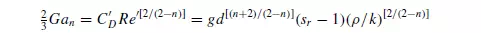
where sr is the ratio of the densities of the particle and of the fluid (ρs/ρ). Equation 3.56 may be written as:

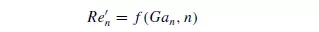
Experimental results comprising about 1000 data points from a large number of sources cover the following range of variables:

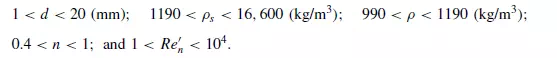
These are satisfactorily correlated by:

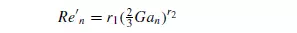
where r1 = 0.1{exp[(0.5/n) − 0.73n] and r2 = (0.954/n) − 0.16 Thus, in equation 3.65 only Re_n includes the terminal falling velocity which may then be calculated for a spherical particle in a power-law fluid.