The drag force acting on a gas bubble or a liquid droplet will not, in general, be the same as that acting on a rigid particle of the same shape and size because circulating currents are set up inside the bubble. The velocity gradient at the surface is thereby reduced and the drag force is therefore less than for the rigid particle. HADAMARD(29) showed that, if the effects of surface energy are neglected, the terminal falling velocity of a drop, as  calculated from Stokes’ law, must be multiplied by a factor Q, to account for the internal circulation, where:

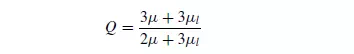
In this equation, μ is the viscosity of the continuous fluid and μl is the viscosity of the fluid forming the drop or bubble. This expression applies only in the range for which

Stokes’ law is valid. If μl/μ is large, Q approaches unity. If μl/μ is small, Q approaches a value of 1.5. Thus the effect of circulation is small when a liquid drop falls in a gas although is large when a gas bubble rises in a liquid. If the fluid within the drop is very viscous, the amount of energy which has to be transferred in order to induce circulation is large and circulation effects are therefore small.  Hadamard’s work was later substantiated by BOND(30) and by BOND and NEWTON(31) who showed that equation 3.51 is valid provided that surface tension forces do not play a large role. With very small droplets, the surface tension forces tend to nullify the tendency for circulation, and the droplet falls at a velocity close to that of a solid sphere. In addition, drops and bubbles are subject to deformation because of the differences

in the pressures acting on various parts of the surface. Thus, when a drop is settling in a still fluid, both the hydrostatic and the impact pressures will be greater on the

forward face than on the rear face and will tend to flatten the drop, whereas the viscous drag will tend to elongate it. Deformation of the drop is opposed by the surface tension forces so that very small drops retain their spherical shape, whereas large drops may be considerably deformed and the resistance to their motion thereby increased. For drops above a certain size, the deformation is so great that the drag force increases at the same rate as the volume, and the terminal falling velocity therefore becomes independent of size. GARNER and SKELLAND(32,33) have shown the importance of circulation within a drop in determining the coefficient of mass transfer between the drop and the surrounding medium. The critical Reynolds number at which circulation commences has been shown(32) to increase at a rate proportional to the logarithm of viscosity of the liquid constituting the drop and to increase with interfacial tension. The circulation rate may be influenced by mass transfer because of the effect of concentration of diffusing material on both the interfacial tension and on the viscosity of the surface layers. As a result of circulation the falling velocity may be up to 50 per cent greater than for a rigid sphere, whereas oscillation of the drop between oblate and prolate forms will reduce the velocity of fall(33). Terminal falling velocities of droplets have also been calculated by HAMIELEC and JOHNSON(34) from approximate velocity profiles at the interface and the values so obtained compare well with experimental values for droplet Reynolds numbers up to 80.