The motion of a particle through a fluid may be traced because the value of the drag factor R_/ρu2 for a given value of the Reynolds number is fixed. The behaviour of a
particle undergoing acceleration or retardation has been the subject of a very large number of investigations, which have been critically reviewed by TOROBIN and GAUVIN(42). The results of different workers are not consistent, although it is shown that the drag factor is often related, not only to the Reynolds number, but also to the number of particle diameters traversed by the particle since the initiation of the motion. A relatively simple approach to the problem, which gives results closely in accord with practical measurements, is to consider the mass of fluid which is effectively given the same acceleration as the particle, as discussed by MIRONER(43). This is only an approximation because elements of fluid at different distances from the particle will not all be subject to the same acceleration. For a spherical particle, this added or hydrodynamic mass is equal to the mass of fluid whose volume is equal to one half of that of the sphere. This can give rise to a very significant effect in the case of movement through a liquid, and can result in accelerations substantially less than those predicted when the added mass is neglected. For movement through gases, the contribution of the added mass term is generally negligible. Added mass is most important for the motion of gas bubbles in a liquid because in that case the surrounding liquid has a much greater density than the bubble. The total mass of particle and associated fluid is sometimes referred to as the virtual mass (m _).
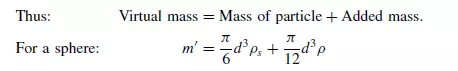

Considering the motion of a particle of mass m in the earth’s gravitational field, at some time t the particle will be moving at an angle α to the horizontal with a velocity
u as shown in Figure 3.7. The velocity u may then be resolved into two components, ˙x and ˙y, in the horizontal and vertical directions. ˙x and ¨x will be taken to denote the first and second derivatives of the displacement x in the X-direction with respect to time, and˙y and ¨y the corresponding derivatives of y.

(b) The drag force which is equal to R_A_ and acts in such a direction as to oppose the motion of the particle. Its direction therefore changes as α changes. Here A
_ is theprojected area of the particle on a plane at right angles to the direction of motion and its value varies with the orientation of the particle in the fluid. The drag force
can be expressed by:
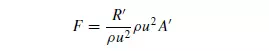

If allowance is now made for the added mass, m_ = m[1 + (ρ/2ρs )] must be substituted for m. Equations 3.77 and 3.78 refer to conditions where the particle is moving in the
positive sense in the X-direction and in the positive (downward) sense in the Y -direction. If the particle is moving in the negative X-direction, the form of solution is unchanged, except that all increments of x will be negative. If, however, the particle is initially moving upwards, the sign of only the frictional term in equation 3.78 is changed and the form of solution will, in general, be different from that for downward movement. Care must therefore be exercised in the application of the equation, particularly if a change of sense may occur during the motion of the particle. It may be noted that the equations of motion for the two directions (X and Y) are
coupled, with ˙x and ˙y appearing in each of the equations. General solutions are therefore not possible, except as will be seen later for motion in the Stokes’ law region.
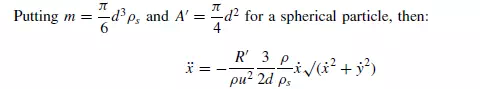
If allowance is made for the added mass and m_ is substituted for m in equation 3.78, then:
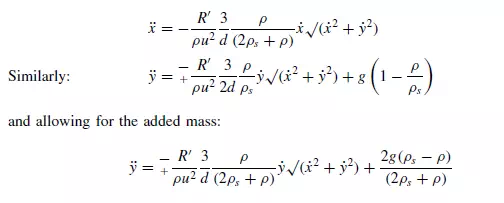
where the minus sign in equations 3.81 and 3.82 is applicable for downward motion and the positive sign for upward motion (with downwards taken as the positive sense).

