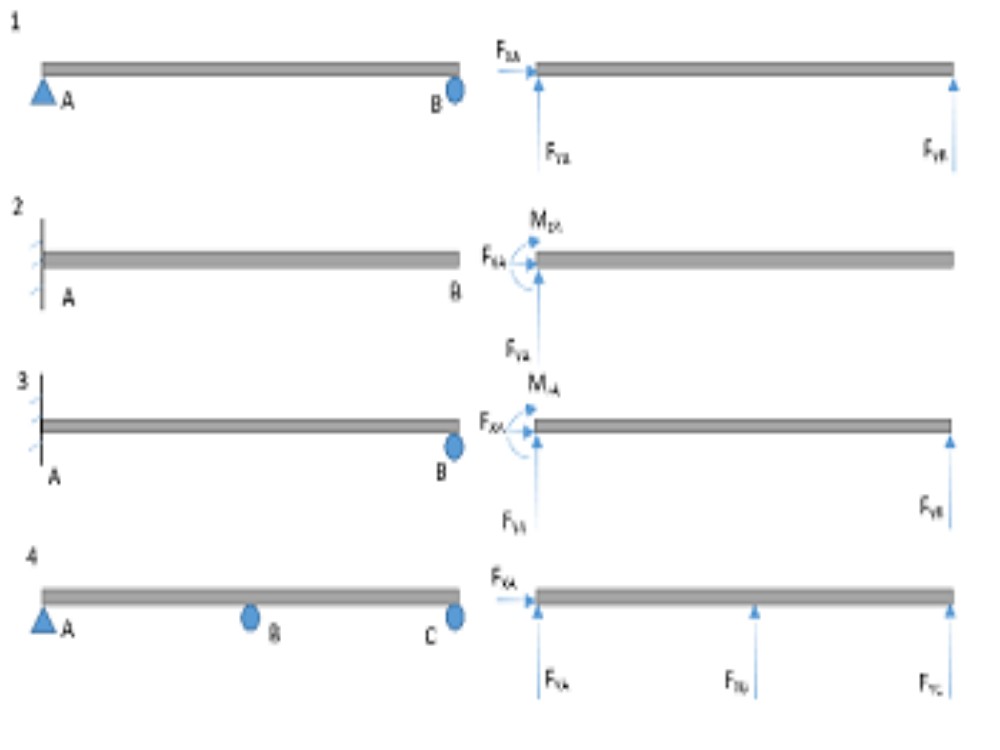
The key to resolving our predicament, when faced with a statically indeterminate problem – one in which the equations of static equilibrium do not suffice to determine a unique solution – lies in opening up our field of view to consider the displacements of points in the structure and the deformation of its members. This introduces new variables, a new genera of flora and fauna, into our landscape; for the truss structure the species of node displacements and the related species of uniaxial member strains must be engaged. For the frame structure made up of beam elements, we must consider the slope of the displacement and the related curvature of the beam at any point along its length. For the shaft in torsion we must consider the rotation of one cross section relative to another.
Displacements you already know about from your basic course in physics – from the section on Kinematics within the chapter on Newtonian Mechanics. Displacement is a vector quantity, like force, like velocity; it has a magnitude and direction. In Kinematics, it tracks the movement of a physical point from some location at time t to its location at a subsequent time, say t +δt, where the term δt indicates a small time increment. Here, in this text, the displacement vector will, most often, represent the movement of a physical point of a structure from its position in the undeformed state of the structure to its position in its deformed state, from the structure’s unloaded configuration to its configuration under load. These displacements will generally be small relative to some nominal length of the structure. Note that previously, in applying the laws of static equilibrium, we made the tacit assumption that displacements were so small we effectively took them as zero; that is, we applied the laws of equilibrium to the undeformed body. 1 There is nothing inconsistent in what we did there with the tack we take now as long as we restrict our attention to small displacements.
That is, our equilibrium equations taken with respect to the undeformed configuration remain valid even as we admit that the structure deforms. Although small in this respect, the small displacement of one point relative to the small displacement of another point in the deformation of a structural member can engender large internal forces and stresses. In a first part of this chapter, we do a series of exercises – some simple, others more complex – but all involving only one or two degrees of freedom; that is, they all concern systems whose deformed configuration is defined by but one or two displacements (and/or rotations). In the final part of this chapter, we consider indeterminate truss structures – systems which may have many degrees of freedom. In subsequent chapters we go on to resolve the indeterminacy in our study of the shear stresses within a shaft in torsion and in our study of the normal and shear stresses within a beam in bending.
Resolving indeterminacy: Some Simple Systems.
If we admit displacement variables into our field of view, then we must necessarily learn how these are related to the forces which produce or are engendered by them. We must know how force relates to displacement. Force-displacement, or constitutive relations, are one of three sets of relations upon which the analysis of indeterminate systems is built. The requirements of force and moment equilibrium make up a second set; compatibility of deformation is the third.
Now compatibility of deformation: The question is, how are the three displacements related. Clearly they must be related; we can not choose them independently one from another, e.g., taking the displacements of the end springs as downward and the displacement of the midpoint as upwards. This could only be the case if the block had fractured into pieces. No, this can’t be. We insist on compatibility of deformation.