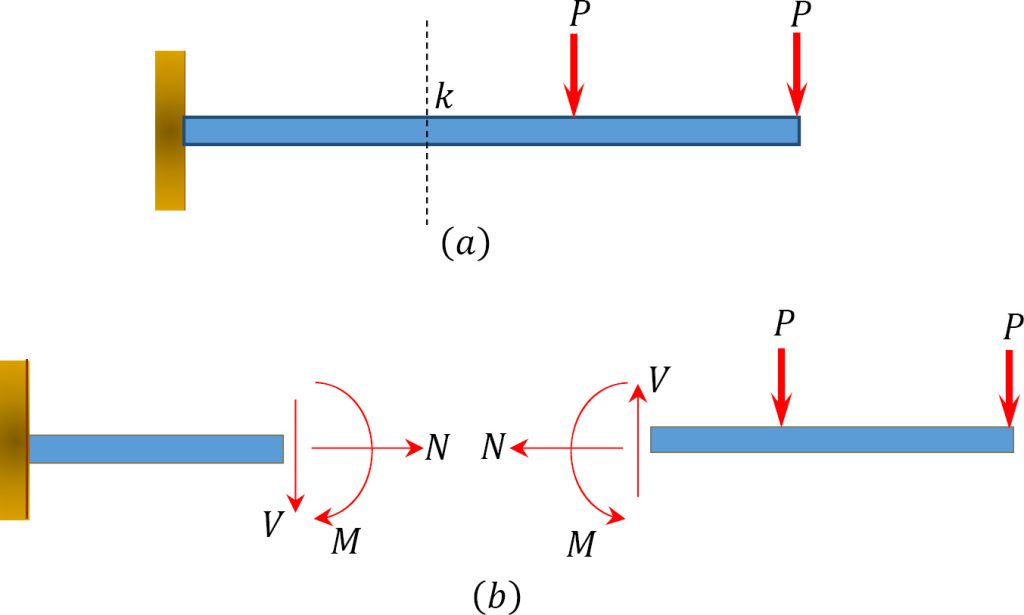
A beam is a structural element like the truss member but, unlike the latter, it is designed, fabricated, and assembled to carry a load in bending 5. In this section we will go as far as we can go with our current vocabulary of force, couple, and moment and with our requirements of static equilibrium, attempting to explain what bending is, how a beam works, and even when it might fail.
The Cantilever according to Galileo
You, no doubt, know what a beam is in some sense, at least in some ordinary, everyday sense. Beams have been in use for a long time; indeed, there were beams before there were two-force members. The figure below shows a seventeenth century cantilever beam. It appears in a book written by Galileo, his Dialogue Concerning Two New Sciences.
Galileo wanted to know when the cantilever beam would break. He asked: What weight, hung from the end of the beam at C, would cause failure? You might wonder about Galileo’s state of mind when he posed the question. From the looks of the wall it is the latter whose failure he should be concerned with, not the beam. No. You are reading the figure incorrectly; you need to put on another special pair of eyeglasses that filter out the shrubbery and the decaying wall and allow you to see only a cantilever beam, rigidly attached to a rigid support at the end AB. These glasses will also be necessary in what follows, so keep them on.
Galileo had, earlier in his book, discussed the failure of what we would call a bar in uniaxial tension. In particular, he claimed and argued that the tensile force F σ = F/A required for failure is proportional to the cross sectional area of the bar, just as we have done. We called the ratio of force to area a “stress”. Galileo did not use our language but he grasped, indeed, might be said to have invented the concept, at least with respect to this one very important trait – stress as a criterion for failure of a bar in tension. Galileo’s achievement in analyzing the cantilever beam under an end load lay in relating the end load at failure to the failure load of a bar in uniaxial tension.
Of course the bar had to be made of the same material. His analysis went as follows: He imagined the beam to be an angular lever pivoted at B. The weight, W, was suspended at one end of the lever, at the end of the long arm BC. A horizontally directed, internal, tensile force – let us call it F – acted along the other shorter, AB vertical arm of the lever AB. Galileo claimed this force acted at a point half way up the lever arm and provided the internal resistance to fracture.
Look back at Galileo’s figure with your special glasses on. Focus on the beam. See now the internal resistance acting along a plane cut through the beam at AB. Forget the possibility of the wall loosening up at the root of the cantilever. Take a peek ahead at the next more modern figure if you are having trouble seeing the internal force resultant acting on the section AB.
According to Galileo, the beam will fail when the ratio of FAB to the cross sectional area reaches a particular, material specific value6. This ratio is what we have called the failure stress in tension. From the above equation we see that, for members with the same cross section area, the end load, W, to cause failure of the member acting as a cantilever is much less than the load, FAB,which causes failure of the member when loaded axially, as a truss member (by the factor of (1/2)h/L).