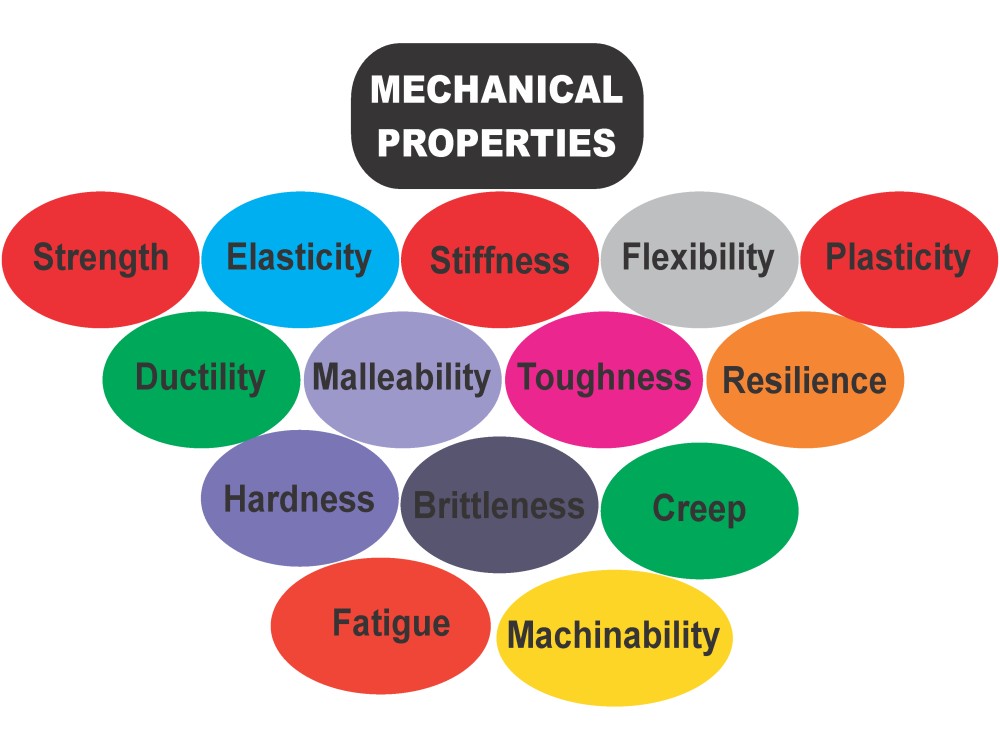
Up until now we have not said much about the way structures behave in the socalled “real world”. Our focus has been on abstract concepts and pictures, with generous use made of mathematics in the formulation and solution of problems. There have been exceptions: We have talked about the properties of a rod, how we could measure the stress at which it would yield. We have talked about linear force/deflection relations and how we could measure the rod’s stiffness, k. But our elaboration and application of the principles of equilibrium and compatibility of deformation have not required any reference to the things of the material world:
Compatibility of deformation is a matter of the displacement of points, their absolute and relative displacement (when we talk about strain). Equilibrium of force and of moment concerns concepts that are just as abstract as displacements of points and rotations of infinitessimal line segments – if not more so. Constructing a free body diagram is an abstract, intellectual activity. No one goes out and actually cuts through the truss to determine the forces within its members.
Stress/Strain Relations
We want to develop a set of stress/strain relations for a continuous body, equations which apply at each and every point throughout the continuum. In this we will restrict our attention, at least in this chapter, to certain type of materials namely homogeneous, linear, elastic, isotropic bodies.
We have talked about stress at a point. W e drew a figure like the one at the right to help us visualize the nature of the normal and shear components of stress at a point. We say the state of stress is fully specified by the normal components, σx, σy σz and the shear components σxy=σyx, σyz=σzy σxz=σzx.
With these restrictions and a heavy dose of symmetry, we will be able to construct a set of stress/strain equations that will apply to many structural materials. This we do now, performing a sequence of thought experiments in which we apply to an element of stuff at a point each stress component in turn and imagine what strains will be engendered, which ones will not. Again, symmetry will be crucial to our constructions. We start by applying the normal stress component σx alone. We expect to see some extensional strain εx.
This we take as proportional to the normal stress we apply, in accord with the second bullet above; that is we set In this we have made use of another bit of real experimental evidence in designating the constant of proportionality in the relationship between the extensional strain in the direction of the applied normal stress to be the elastic, or Young’s modulus, E. We might not anticipate normal strains in the other two coordinate directions but there is nothing to rule them out, so we posit an εy and an εz. Now εy and εz, because of the indifference of the material to the orientation of the y and the z axis,– that is, from symmetry– must be equal. We can say nothing more on the basis of our symmetrical thoughts alone.