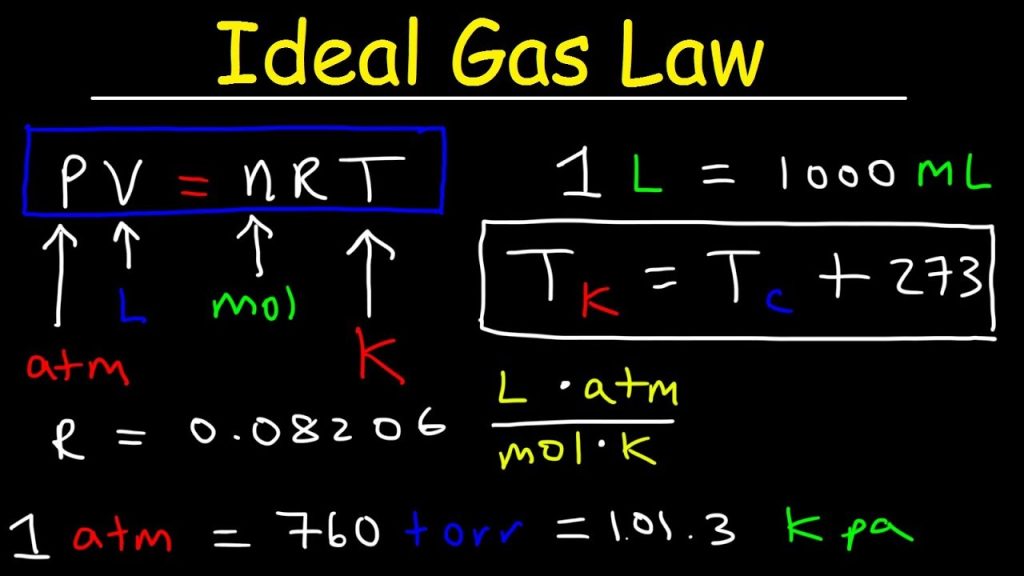
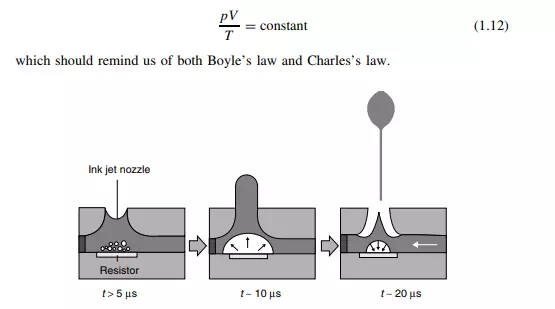
A bubble-jet printer is one of the more useful and versatile inventions of the last decade. The active component of the printer is the ‘head’ through which liquid ink passes before striking the page. The head moves from side to side over the page. When the ‘head’ is positioned above a part of the page to which an image is required, the computer tells the head to eject a tiny bubble of ink. This jet of ink strikes the page to leave an indelible image. We have printing. The head is commonly about an inch wide, and consists of a row of hundreds of tiny pores (or ‘capillaries’), each connecting the ink reservoir (the cartridge) and the page. The signals from the computer are different for each pore, allowing different parts of the page to receive ink at different times. By this method, images or letters are formed by the printer.
The pores are the really clever bit of the head. Half-way along each pore is a minute heater surrounded by a small pocket of air. In front of the heater is a small bubble of ink, and behind it is the circuitry of the printer, ultimately connecting the heater to the computer. One such capillary is shown schematically in Figure 1.8. Just before the computer instructs the printer to eject a bubble of ink, the heater is activated, causing the air pocket to increase in temperature T at quite a rapid rate. The temperature increase causes the air to expand to a greater volume V . This greater volume increases the pressure p within the air pocket. The enhanced air pressure p is sufficient to eject the ink bubble from the pore and onto the page. This pressure-activated ejection is similar to spitting. This ejection of ink from a bubble-jet printer ingeniously utilizes the interconnectedness of pressure p, volume V and temperature T . Experiments with simple gases show how p, T and V are related by the relation.
If there is exactly 1 mol of gas, the pressure is expressed in pascals (Pa), the temperature is in kelvin and the volume is in cubic metres (both SI units), then the value of the constant is 8.314 J K−1 mol−1 . We call it the gas constant and give it the symbol R. (Some old books may call R the ‘universal gas constant’, ‘molar gas constant’ or just ‘the gas constant’. You will find a discussion about R on p. 54) More generally, Equation (1.12) is rewritten as
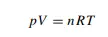
where n is the number of moles of gas. Equation (1.13) is called the ideal-gas equation (or, sometimes, in older books the ‘universal gas equation’). The word ‘ideal’ here usually suggests that the gas in question obeys Equation (1.13). Worked Example 1.3 What is the volume of 1 mol of gas at a room temperature of 25 ◦ C at an atmospheric pressure of 105 Pa? First, we convert the data into the correct SI units. In this example, only the temperature needs to be converted. From Equation (1.7), the temperature is 298 K. Secondly, we rearrange Equation (1.13) to make V the subject, by dividing both sides