The question, ‘What is pressure?’ is another odd question, but is not too difficult to answer. The constituent particles of a substance each have energy. In practice, the energy is manifested as kinetic energy – the energy of movement – and explains why all molecules and atoms move continually as an expression of that kinetic energy. This energy decreases as the temperature decreases. The particles only stop moving when cooled to a temperature of absolute zero: 0 K or −273.15 ◦ C. The particles are not free to move throughout a solid substance, but can vibrate about their mean position.
The frequency and amplitude of such vibration increases as the temperature rises. In a liquid, lateral motion of the particles is possible, with the motion becoming faster as the temperature increases. We call this energy translational energy. Furthermore, as the particles acquire energy with increased temperature, so the interactions (see Chapter 2) between the particles become comparatively smaller, thereby decreasing the viscosity of the liquid and further facilitating rapid motion of the particles.
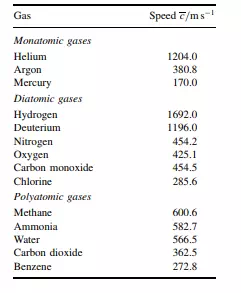
When the interactions become negligible (comparatively), the particles can break free and become gaseous. And each particle in the gaseous state can move at amazingly high speeds; indeed, The gas particles are widely separated. they are often supersonic. For example, an average atom of helium travels at a mean speed of 1204 m s−1 at 273.15 K. Table 1.4 lists the mean speeds of a few other gas molecules at 273.15 K. Notice how heavier molecules travel more slowly, so carbon dioxide has a mean speed of 363 m s−1 at the same temperature. This high speed of atomic and molecular gases as they move is a manifestation of their enormous kinetic energy. It would not be possible to travel so fast in a liquid or solid because they are so much denser – we call them condensed phases.
The separation between each particle in gas is immense, and Particles of gas travel fast and in straight lines, unless they collide. usually thousands of times greater than the diameter of a single gas particle. In fact, more than 99 per cent of a gas’s volume is empty space. The simple calculation in Worked Example 1.5 demonstrates this truth.