If no heat was distributed, then our faces and those parts closest to the fire We often see this relationship called merely the ‘Boltzmann distribution’, after the Austrian Physicist Ludwig Boltzmann (1844– 1906), who played a pivotal role in marrying thermodynamics with statistical and molecular physics. would quickly become unbearably hot, while the remainder of our flesh would continue to feel cold. Heat conducts through the body principally by the fire warming the blood on the surface of the skin, which is then pumped to other parts of the body through the circulatory system.

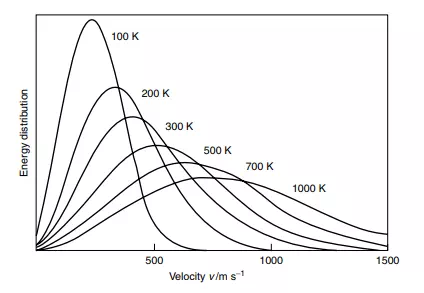
The energy in the warmed blood is distributed within cooler, internal tissues. It is important to note how the heat energy is distributed around the body, i.e. shared and equalized. Nature does not like diversity in terms of energetic content, and provides many mechanisms by which the energy can be ‘shared’. We shall discuss this aspect of thermochemistry in depth within Chapter 4. We can be certain that molecules do not each have the same energy, but a distribution of energies. The graph in Figure 1.9 concerns the energies in a body.

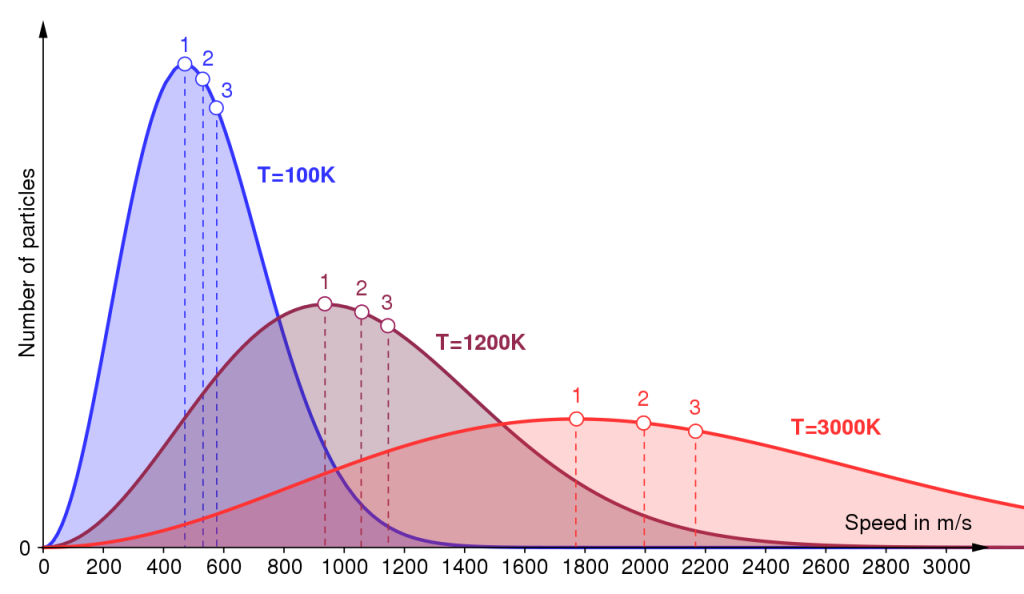
The x-axis gives the range of energies possible, and the y-axis represents the number of particles in the body (molecules, atoms, etc.) having that energy. The graph clearly shows how few particles possess a large energy and how a few particles have a tiny energy, but the majority have lesser energies. We call this spread of energies the ‘Maxwell–Boltzmann distribution’.

All speeds are found at all temperatures, but more molecules The thermodynamic temperature is the sole variable required to define the Maxwell– Boltzmann distribution: raising the temperature increases the spread of energies. travel at faster speeds at the higher temperatures. The distribution law depicted in Figure 1.9 may be modelled mathematically, to describe the proportions of molecules of molar mass M with energies E in the range E to E + dE that exist in

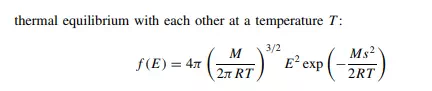
where f on the far left indicates the ‘function’ that is to be applied to the variable E: the mathematical nature of this function is given by the right-hand side of the equation. So, in summary, we feel warmer in front of a fire because energy is distributed between those parts facing the flames and the more hidden tissues within.