The pressure p of the air above any point on the Earth’s surface relates ultimately to the amount of air above it. If we are standing high up, for example on the top of a tall mountain, there is less air between us and space for gravity to act upon. Conversely, if we stand at the bottom of the Grand Canyon (one of the lowest places on Earth) then more air separates us from space, causing the air pressure p to be much greater.

A barometer is an instrument designed to measure air pressure p. It consists of a pool of liquid mercury in a trough. A long, thin glass tube (sealed at one end) is placed in the centre of the trough with its open-side beneath the surface of the liquid; see Figure 1.2. The pressure of the air acts as a force on the surface of the mercury, forcing it up and into the capillary within the tube. If the air pressure is great, then the force of the air on the mercury is also great, causing much mercury up the tube. A lower pressure is seen as a shorter length h of mercury in the tube. By performing experiments at different pressures, it is easy to prove the existence of a relationship between the air pressure p and the height h of the mercury column.

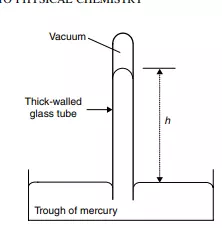
In practice, a barometer is merely an instrument on which we look at the length of the column of mercury h and, via Equation (1.1), calculate the air pressure p. The magnitude of h is in direct relation to the pressure p. We ascertain the magnitude of h if we need to know the air pressure p. While physical chemistry can appear to be horribly mathematical, in fact the matheWe might see this situation written mathematically as, h = f(p), where the ‘=’ means ‘is not equal to’. In other words, h is not a function of p in a poor barometer. matics we employ are simply one way (of many) to describe the relationships between variables.

Often, we do not know the exact nature of the function until a later stage of our investigation, so the complete form of the relationship has to be discerned in several stages. For example, perhaps we first determine the existence of a linear equation, like Equation (1.1), and only then do we seek to measure an accurate value of the constant c. But we do know a relationship holds, because there is a response. We would say there was no relationship if there was no response. For example, imagine we had constructed a poor-quality barometer (meaning it does not follow Equation (1.1)) and gave it a test run. If we could independently verify that the pressure p had been varied over a wide range of values yet the length of the mercury h in the barometer did not change, then we would say no relationship existed between p and h.