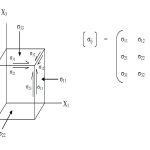
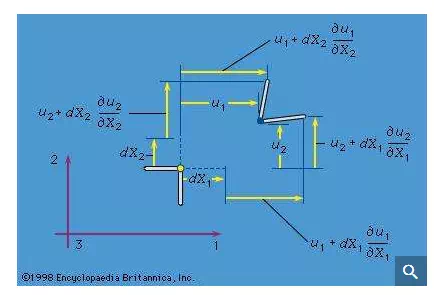
The small strains, or infinitesimal strains, εij are appropriate for situations with |∂uk/∂Xl|<< 1 for all k and l. Two infinitesimal material fibres, one initially in the 1 direction and the other in the 2 direction, are shown in Figure 6 as dashed lines in the reference configuration and as solid lines in the deformed configuration. To first-order accuracy in components of [∂u/∂X], the extensional strains of these fibres are ε11 = ∂u1/∂X1 and ε22 = ∂u2/∂X2, and the reduction of the angle between them is γ12 = ∂u2/∂X1 + ∂u1/∂X2. For the shear strain denoted ε12, however, half of γ12 is used. Thus, considering all extensional and shear strains associated with infinitesimal fibres in the 1, 2, and 3 directions at a point of the material, the set of strains is given by
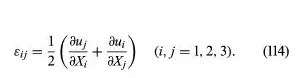
The εij are symmetric—i.e., εij = εji—and form a second-rank tensor (that is, if Cartesian reference axes 1′, 2′, and 3′ were chosen instead and the εkl′ were determined, then the εkl′ are related to the εij by the same equations that relate the stresses σkl′ to the σij). These mathematical features require that there exist principal strain directions; at every point of the continuum it is possible to identify three mutually perpendicular directions along which there is purely extensional strain, with no shear strain between these special directions. The directions are the principal strain directions, and the corresponding strains include the least and greatest extensional strains experienced by fibres through the material point considered. Invariants of the strain tensor may be defined in a way paralleling those for the stress tensor.
An important fact to note is that the strains cannot vary in an arbitrary manner from point to point in the body. This is because the six strain components are all derivable from three displacement components. Restrictions on strain resulting from such considerations are called compatibility relations; the body would not fit together after deformation unless they were satisfied. Consider, for example, a state of plane strain in the 1, 2 plane (so that ε33 = ε23 = ε31 = 0). The nonzero strains ε11, ε22, and ε12 cannot vary arbitrarily from point to point but must satisfy
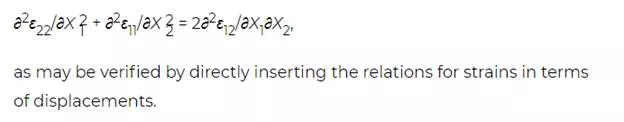
When the smallness of stretch and rotation of line elements allows use of the infinitesimal strain tensor, a derivative ∂/∂Xi will be very nearly identical to ∂/∂xi. Frequently, but not always, it will then be acceptable to ignore the distinction between the deformed and undeformed configurations in writing the governing equations of solid mechanics. For example, the differential equations of motion in terms of stress are rigorously correct only with derivatives relative to the deformed configuration, but, in the circumstances considered, the equations of motion can be written relative to the undeformed configuration. This is what is done in the most widely used variant of solid mechanics, in the form of the theory of linear elasticity. The procedure can be unsatisfactory and go badly wrong in some important cases, however, such as for columns that buckle under compressive loadings or for elastic-plastic materials when the slope of the stress versus strain relation is of the same order as existing stresses. Cases such as these are instead best approached through finite deformation theory.