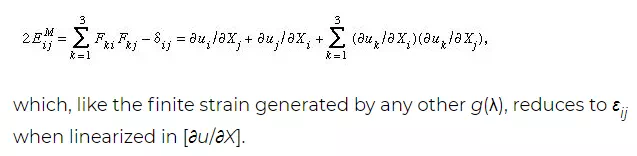In the theory of finite deformations, extension and rotations of line elements are unrestricted as to size. For an infinitesimal fibre that deforms from an initial point given by the vector dX to the vector dx in the time t, the deformation gradient is defined by Fij = ∂xi(X, t)/∂Xj; the 3 × 3 matrix [F], with components Fij, may be represented as a pure deformation, characterized by a symmetric matrix [U], followed by a rigid rotation [R]. This result is called the polar decomposition theorem and takes the form, in matrix notation, [F] = [R][U]. For an arbitrary deformation, there exist three mutually orthogonal principal stretch directions at each point of the material; call these directions in the reference configuration N(I), N(II), N(III), and let the stretch ratios be λI, λII, λIII. Fibres in these three principal strain directions undergo extensional strain but have no shearing between them. Those three fibres in the deformed configuration remain orthogonal but are rotated by the operation [R].
As noted earlier, an extensional strain may be defined by E = g(λ), where g(1) = 0 and g′(1) = 1, with examples for g(λ) given above. A finite strain tensor Eij may then be defined based on any particular function g(λ) by Eij = g(λI)Ni(I)Nj(I) + g(λII)Ni(II)Nj(II) + g(λIII)Ni(III)Nj(III). Usually, it is rather difficult to actually solve for the λ’s and N’s associated with any general [F], so it is not easy to use this strain definition. However, for the special choice identified as gM(λ) = (λ2 − 1)/2 above, it may be shown that