with More than One Component Almost all real systems involve multicomponent mixtures that require a slightly different approach for solving material balance problems than a system with a single component. The application of Equation (3.2) to a system with a single component results in a single material balance equation. For systems with more than one component, you can write more than one material balance equation.
Normally for multicomponent systems, you can write a separate material balance equation for each component present in the system plus one additional material balance equation based on the total mass of the system, but one of the set will be dependent (redundant). In any event, the issue of selecting the right material balance equations to use is addressed in Section 3.2 in the eighth step of the generalized strategy for solving material balance problems. All the cases considered so far have illustrated the flow of water—a single component. Suppose the input to a vessel contains more than one component, such as 100 kg/min of a 50% water and 50% sugar (sucrose, C12H22O11 , MW 342.3) mixture. As indicated in Figure 3.4, the vessel initially contains 1000 kg of water, and the exit stream flow is 100 kg/min of water and sugar.
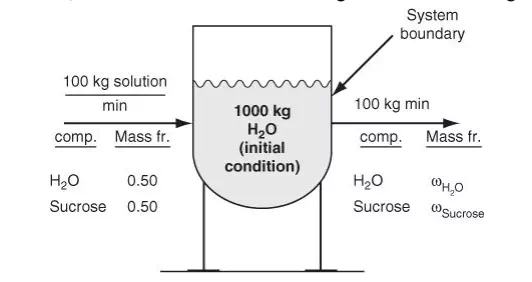
How would the material balance for the process in Figure 3.4 differ from the material balances that would be used for the systems displayed in Figures 3.1 through 3.3? Certainly you can write a total material balance for the process as before. Will it be a steady-state balance? Yes. In addition, because two components exist, you can write two independent component material balances, one for water and one for sucrose. Will they be steady-state balances? No, because sugar starts to accumulate in the system while water is depleted after the addition of the sugar solution. Now look at the mixer shown in Figure 3.5, an apparatus that mixes two streams to increase the concentration of NaOH in a dilute solution. We will use the values of the components listed in Figure 3.5 to show how the total and component balances for mass and moles can be written using Equation (3.2). Note: If the tank is well mixed, the concentration of a component in the output stream will be the same as the concentration of the component inside the tank during mixing, an assumption frequently made that is relatively accurate if adequate mixing is used.
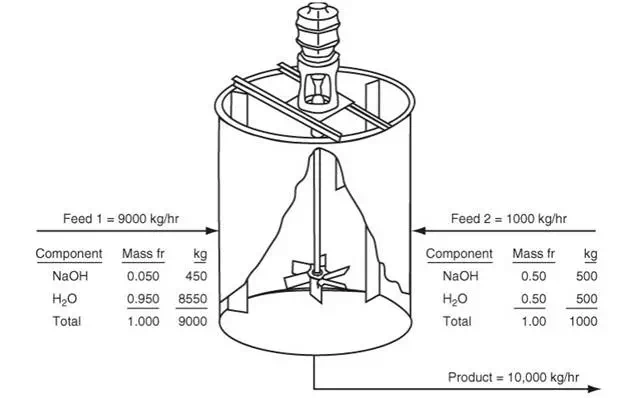
Let’s take a convenient basis of 1 hr. Then the values shown in kilograms in the figure next to the mass fractions show the results of 1 hr of mixing. Could you select another basis? Of course, such as 1 min, 1000 kg, and so on, but the chosen basis is the simplest one. Let’s also assume that this process is at steady state. What does this assumption mean with respect to the material balances? No net accumulation occurs overall. We do not know how much material is in the mixing tank, but does that matter? No, because we are interested only in determining what is leaving the process. Applying Equation (3.3), remembering that the accumulation is equal to zero, yields.