By system we mean any arbitrary portion of or a whole process you want to consider for analysis. You can define a system such as a reactor, a section of a pipe, or an entire refinery by stating in words what the system is. Or you can define the limits of the system by drawing the system boundary, which is a line that encloses the portion of the process that you want to analyze. The boundary could coincide with the outside of a piece of equipment or some section inside the equipment. Now, let’s focus on some important characteristics associated with systems.
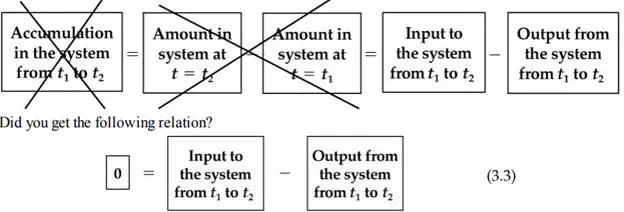
Closed System or Process Figure 3.1a shows a two-dimensional view of a three-dimensional vessel holding 1000 kg of H2O. Note that material neither enters nor leaves the vessel; that is, no material crosses the system boundary. Figure 3.1a represents a closed system. Changes can take place inside the closed system, but no mass exchange occurs with the surroundings. Apply Equation (3.2) to the system shown in Figure 3.1a. What is the accumulation? Did you decide that the accumulation is zero?
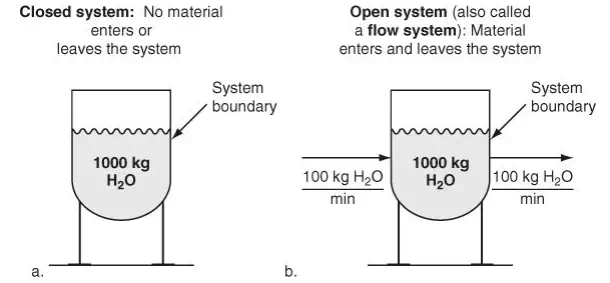
100 kg/min and withdraw water at the rate of 100 kg/min as indicated in Figure 3.1b. Figure 3.1b is an example of an open system (also called a flow system) because the material crosses the system boundary. Apply Equation (3.2) again to Figure 3.1b. What is the value of the accumulation? In this case the accumulation is zero because the total inlet flow is equal to the total outlet flow. Steady-State System or Process What does steady-state mean? A variable, such as an amount of material or a property, is in the steady state if the value of that variable is invariant (does not change) with time.
If you look at Figure 3.1b, you will note that the flow rates in and out are just water and presumably constant and equal, respectively; hence the accumulation is zero, and the system is in the steady state. Most industrial processes under normal conditions are not really steady-state because the values of the variables involved when measured fluctuate continuously due to low-level disturbances to the process and the action of the control systems to counteract these disturbances. Yet the operation of such processes is frequently referred to as “steady-state behavior.”
Consequently, we will have to distinguish between an operating process and the model, or mathematical description, of the process. Thus, a looser concept of the steady state, one that should properly be called pseudo steady-state (meaning that it is not truly steady-state but for convenience is treated as steady-state) or perhaps quasi steady-state (meaning effectively behaving as though it were steady-state), will in this book mean for the selected time interval that (a) the accumulation term in Equation (3.1) will be zero, and (b) the rates of flow and the properties of the flows can be assumed to be constant even if they are not. Also, we will suppress the prefix pseudo or quasi and just use steady-state for convenience. With this assumption, the main criterion of steady-state will be that the accumulation term in Equations (3.1) and (3.2) is zero.
involves mass for the flows and initial and final conditions. However, mass is not the only quantity that is included in the category of “material balance.” The term material can apply to moles or any quantity that is conserved. As an example, look at Figure 3.2 in which we have converted all of the mass quantities in Figure 3.1b to their equivalent in moles.