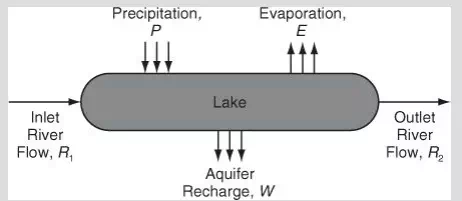
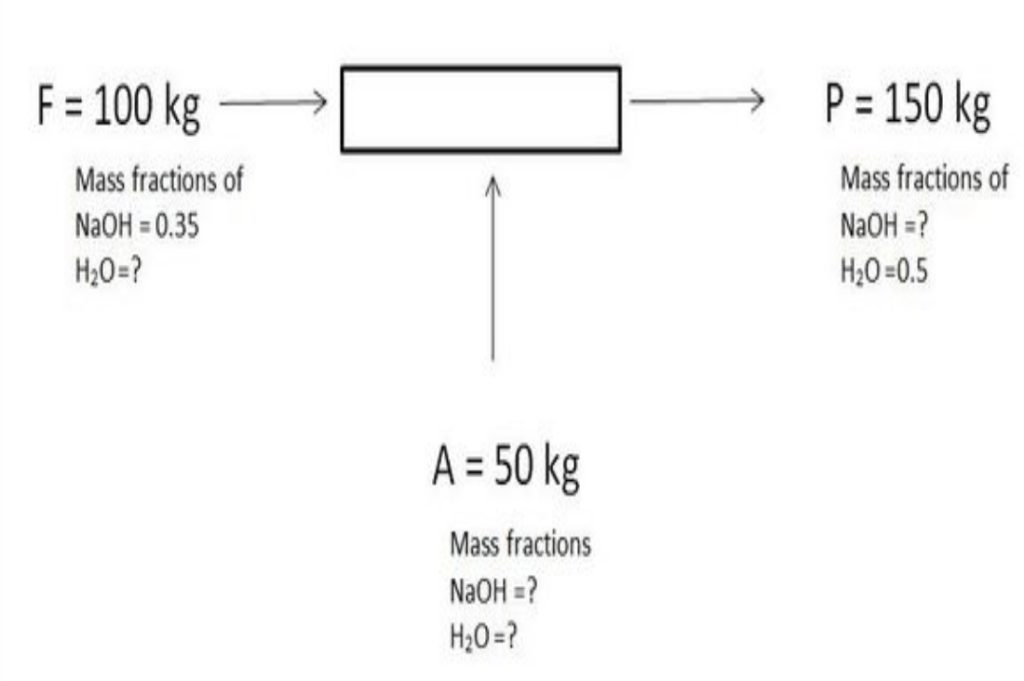
To begin our discussion of the material balance equation, let’s consider a system composed of a single component for which there are no chemical reactions occurring. Then, the general equation, Equation (3.1), with the absence of reaction, reduces to

In other words, the accumulation inside a system is equal to the difference between what enters and what leaves the system. All the comments in Section 3.1.1 with regard to converting flow rates into flows by picking a suitable time interval as the basis apply equally well to Equation (3.2). Now for a test. Here is a puzzle involving money balances. Three students rent a room the night before the game and pay the desk clerk $60. A new clerk comes on duty and finds that the discount rate for students should have been $55. The new clerk gives the bellhop $5 to return to the students, but the bellhop, not having change and being slightly dishonest, returns only $1 to each student and keeps the remaining $2. Now each student paid $20 – $1 = $19, and 3 × $19 = $57 paid in total. The bellhop kept $2 for a total of $59. What happened to the other $1? Apply what you have learned so far to solve the puzzle. It provides a good simple illustration of the confusion that can be cleared up by making a material (here, dollars) balance. (If the puzzle stumps you, look at the end of the next Self-Assessment Test for the answer.)