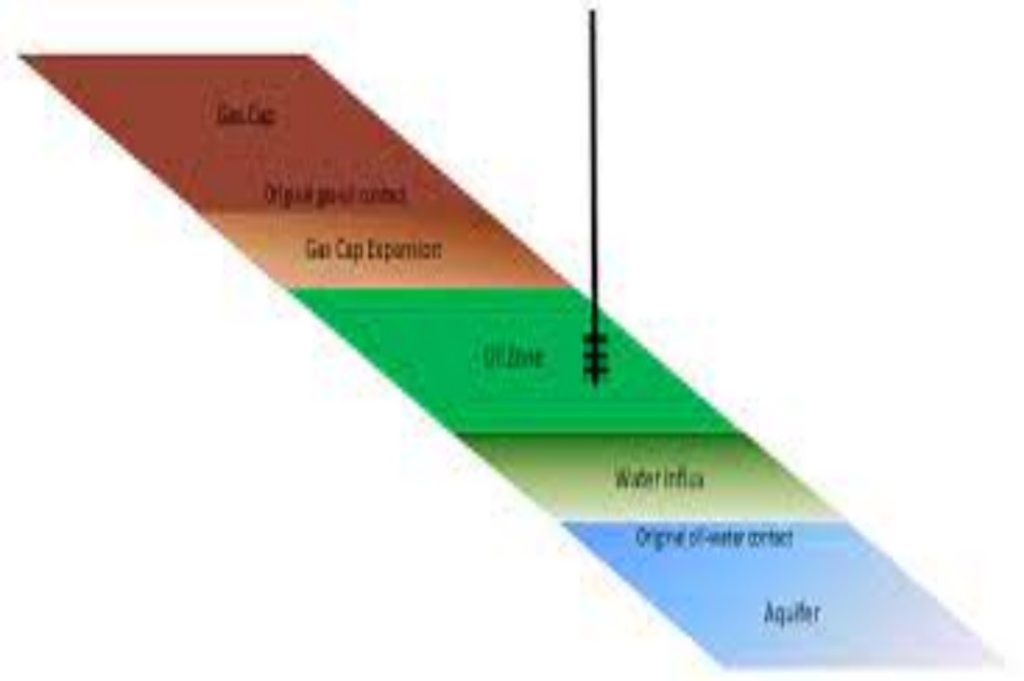
You can get a good idea of what is involved in making a material balance by examining a bank statement such as the following one that illustrates the changes in a checking account
The checking account initially has a balance of $1253.89, which is the initial condition of the account. Deposits (what goes in, the inputs) add to the balance, and withdrawals and checks (what goes out, the outputs) are subtracted from the balance. The final condition is the closing balance ($1878.76). The difference between the initial balance and the final balance is the accumulation in the account (which can be negative!). The column headed “Other” represents interest generated by the balance in the account and bank charges that consume some of the balance in the account.
These latter two terms affect the balance but are not withdrawals, checks, or deposits. Can you write an equation in words that expresses the accumulation in the bank account in terms of the initial and final balances, the deposits and withdrawals, and the interest and fees? Finally, the daily balance represents the net effect of the withdrawals, deposits, fees, and interest on the balance since the beginning of the month. Look at the following relation: Accumulation = Final balance – Initial balance = Deposits – Withdrawals + Interest – Fees Industrial processes are quite analogous to the checking account. Material balances pertain to materials rather than money, as you can infer from the name, but the concepts of balancing money and material are exactly the same.
The initial conditions for a process involve the amount of material initially present in the process. Deposits into the checking account are analogous to the flow of material into a process, and withdrawals are analogous to the flow of material out of a process. Accumulation of material in a process is the same as accumulation in the bank account. Generation and consumption terms in a process occur because of chemical reaction.
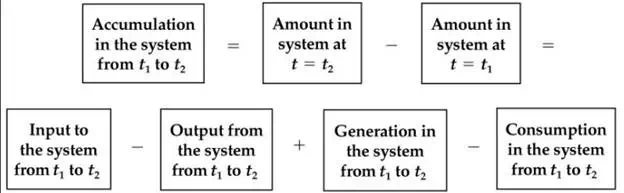
Note that the last two terms, which pertain to generation and consumption of material, are generally included in material balances only for chemical components when chemical reaction occurs in the system, a topic that will be deferred until Chapter 5. Equation (3.1) can be applied to conservation of total mass, mass of a component, moles of a component (but usually not total moles—why?), mass of an atomic species, and moles of an atomic species, but not to volume. Why? Mass is conserved while volume is generally not because different materials have different densities. Did you notice that Equation (3.1) is written in terms of amounts of material, not rates? You can apply it to any selected time interval you want, whether explicitly specified in a problem or not.
By this statement we mean that if a rate is specified in a problem, you can solve the problem on the basis of selecting a convenient time period, or by using 1 or 100 of some quantity in the problem as a basis, and then converting your solution back to the original rate specified in the problem. The form of Equation (3.1) is known as a difference equation (for discrete units of time). The sums of the discrete amounts, as you can observe from the daily transactions in the bank statement, become the amounts involved in each term of Equation (3.1) from the beginning to the end of the selected time interval (one month for the bank statement). The times you select for the final and initial conditions can be any arbitrary interval, but for convenience, if given a flow rate, you usually select an interval such as 1 min or 1 hr as the basis. Variables that are flows will be distinguished from variables that are flow rates by placing an overlay dot on the latter. As an example, F represents a flow and the flow rate.