All the heat transfer problems we have examined have been steady state, but there are often circumstances in which the transient response to heat transfer is critical. An example is the heating up of gas turbine compressors as they are brought up to speed during take-off. The disks that hold the blades are large and take a long time to come to temperature, while the casing is thin and in the path of high velocity compressor flow and thus comes to temperature rapidly.
The result is that the case expands away from the blade tips, sometimes enough to cause serious difficulties with aerodynamic performance. To introduce the topic as well as to increase familiarity with modeling of heat transfer problems, we examine a lumped parameter analysis of an object cooled by a stream. This will allow us to see what the relevant non-dimensional parameters are and, at least in a quantitative fashion, how more complex heat transfer objects will behave. We want to view the object as a “lump” described by a single parameter.
We need to determine when this type of analysis would be appropriate. To address this, consider the temperature difference T1 – Tw between two locations in the object, as shown in Figure
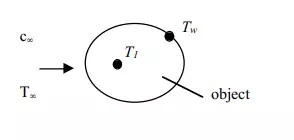
If the heat transfer within the body and from the body to the fluid are of the same magnitude,

The approximation made is to view the object as having a spatially uniform temperature that is a function of time only. Explicitly, T = T(t). The first law applied to the object is (using the fact that for solids cp = cv = c)

The constant a can be seen to be equal to unity to satisfy the initial condition. This form of equation implies that the solution has a heat transfer “time constant” given by hA ρVc τ .
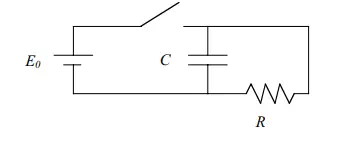
The time constant,τ, is in accord with our “intuition”; high density, large volume, or high specific heat all tend to increase the time constant, while high heat transfer coefficient and large area will tend to decrease the time constant. This is the same form of equation and the same behavior you have seen for the R-C circuit, as shown schematically below. The time dependence of the voltage in the R-C circuit when the switch is opened suddenly is given by the equation + = 0 RC E dt dE . There are, in fact, a number of physical processes which have (or can be modeled as having) this type of exponentially decaying behavior.


Comments are closed