Tortuosity. Although it was implied in the derivation of equation 4.9 that a single value of the Kozeny constant K__ applied to all packed beds, in practice this assumption does not hold. CARMAN(7) has shown that:
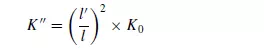
where (l_/l) is the tortuosity and is a measure of the fluid path length through the bedcompared with the actual depth of the bed, K0 is a factor which depends on the shape of the cross-section of a channel through which fluid is passing. For streamline fluid flow through a circular pipe where Poiseuille’s equation applies (given in Volume 1, Chapter 3), K0 is equal to 2.0, and for streamline flow through a rectangle where the ratio of the lengths of the sides is 10 : 1, K0 = 2.65. CARMAN(14) has listed values of K0 for other cross-sections. From equation 4.22 it can be seen that if, say, K0 were constant, then K __ would increase with increase in tortuosity. The reason for K __being near to 5.0 for many different beds is probably that changes in tortuosity from one bed to another have been compensated by changes in K0 in the opposite direction. Wall effect. In a packed bed, the particles will not pack as closely in the region near the wall as in the centre of the bed, so that the actual resistance to flow in a bed of small diameter is less than it would be in an infinite container for the same flowrate per unit area of bed cross-section. A correction factor fw for this effect has been determined experimentally by COULSON(15). This takes the form:
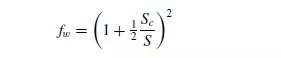
where Sc is the surface of the container per unit volume of bed. Equation 4.9 then becomes:
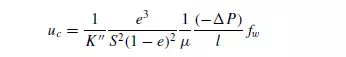
The values of K__ shown on Figure 4.2 apply to equation 4.24.
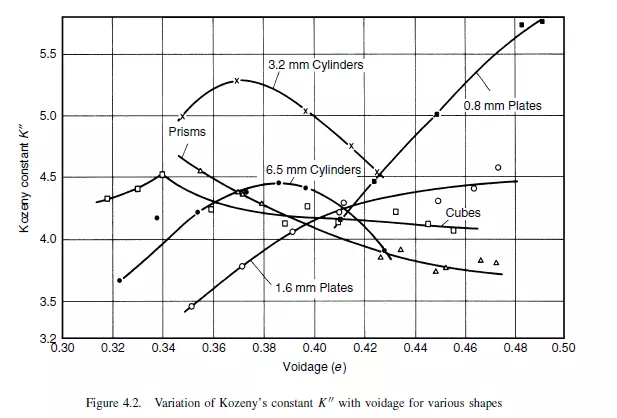
Non-spherical particles. COULSON(15) andWYLLIE and GREGORY(16) have each determined values of K__ for particles of many different sizes and shapes, including prisms, cubes, and plates. Some of these values for K__ are shown in Figure 4.2 where it is seen that they lie between 3 and 6 with the extreme values only occurring with thin plates. This variation of K__ with plates probably arises, not only from the fact that area contact is obtained between the particles, but also because the plates tend to give greater tortuosities. For normal granular materials KIHN(17) and PIRIE(18) have found that K __ is reasonably constant and does not vary so widely as the K__ values for extreme shapes in Figure 4.2. Spherical particles. Equation 4.24 has been tested with spherical particles over a wide range of sizes and K__ has been found to be about 4.8 } 0.3(15,19). For beds composed of spheres of mixed sizes the porosity of the packing can change very rapidly if the smaller spheres are able to fill the pores between the larger ones. Thus COULSON(15) found that, with a mixture of spheres of size ratio 2 : 1, a bed behaves much in accordance with equation 4.19 but, if the size ratio is 5 : 1 and the smaller particles form less than 30 per cent by volume of the larger ones, then K__ falls very rapidly, emphasising that only for uniform sized particles can bed behaviour be predicted with confidence. Beds with high voidage. Spheres and particles which are approximately isometric do not pack to give beds with voidages in excess of about 0.6. With fibres and some ring packings, however, values of e near unity can be obtained and for these high values K__rises rapidly. Some values are given in Table 4.2.
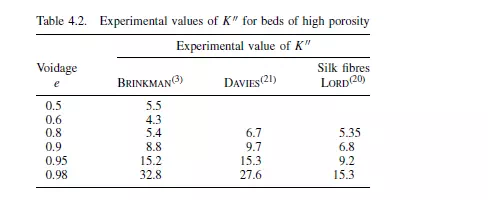
Deviations from the Carman–Kozeny equation (4.9) become more pronounced in these beds of fibres as the voidage increases, because the nature of the flow changes from one of channel flow to one in which the fibres behave as a series of obstacles in an otherwise unobstructed passage. The flow pattern is also different in expanded fluidised beds and the Carman–Kozeny equation does not apply there either. As fine spherical particles move far apart in a fluidised bed, Stokes’ law can be applied, whereas the Carman–Kozeny equation leads to no such limiting resistance. This problem is further discussed by CARMAN(14).
Effect of bed support.
The structure of the bed, and hence K__, is markedly influenced by the nature of the support. For example, the initial condition in a filtration may affect the whole of a filter cake. Figure 4.3 shows the difference in orientation of two beds of cubical particles. The importance of the packing support should not be overlooked in considering the drop in pressure through the column since the support may itself form an important resistance, and by orientating the particles as indicated may also affect the total pressure drop.