Dispersion is the general term which is used to describe the various types of self-induced mixing processes which can occur during the flow of a fluid through a pipe or vessel. The effects of dispersion are particularly important in packed beds, though they are also present under the simple flow conditions which exist in a straight tube or pipe. Dispersion can arise from the effects of molecular diffusion or as the result of the flow pattern existing within the fluid. An important consequence of dispersion is that the flow in a packed bed reactor deviates from plug flow, with an important effect on the characteristics of the reactor.It is of interest to consider first what is happening in pipe flow. Random molecular movement gives rise to a mixing process which can be described by Fick’s law (given in Volume 1, Chapter 10). If concentration differences exist, the rate of transfer of a component is proportional to the product of the molecular diffusivity and the concentration gradient. If the fluid is in laminar flow, a parabolic velocity profile is set up over the crosssection and the fluid at the centre moves with twice the mean velocity in the pipe. This can give rise to dispersion since elements of fluid will take different times to traverse the length of the pipe, according to their radial positions. When the fluid leaves the pipe, elements that have been within the pipe for very different periods of time will be mixed together. Thus, if the concentration of a tracer material in the fluid is suddenly changed, the effect will first be seen in the outlet stream after an interval required for the fluid at the axis to traverse the length of the pipe. Then, as time increases, the effect will be evident in the fluid issuing at progressively greater distances from the centre. Because the fluid velocity approaches zero at the pipe wall, the fluid near the wall will reflect the change over only a very long period. If the fluid in the pipe is in turbulent flow, the effects of molecular diffusion will be supplemented by the action of the turbulent eddies, and a much higher rate of transfer of material will occur within the fluid. Because the turbulent eddies also give rise to momentum transfer, the velocity profile is much flatter and the dispersion due to the effects of the different velocities of the fluid elements will be correspondingly less. In a packed bed, the effects of dispersion will generally be greater than in a straight tube. The fluid is flowing successively through constrictions in the flow channels and then through broader passages or cells. Radial mixing readily takes place in the cells because the fluid enters them with an excess of kinetic energy, much of which is converted into rotational motion within the cells. Furthermore, the velocity profile is continuously changing within the fluid as it proceeds through the bed. Wall effects can be important in a packed bed because the bed voidage will be higher near the wall and flow will occurpreferentially in that region.

At low rates of flow the effects of molecular diffusion predominate and cell mixing contributes relatively little to the dispersion. At high rates, on the other hand, a realistic

model is presented by considering the bed to consist of a series of mixing cells, the dimension of each of which is of the same order as the size of the particles forming

the bed. Whatever the mechanism, however, the rate of dispersion can be conveniently described by means of a dispersion coefficient. The process is generally anisotropic, except at very low flowrates; that is the dispersion rate is different in the longitudinal and radial directions, and therefore separate dispersion coefficients DL and DR are generally used to represent the behaviour in the two directions. The process is normally linear, with the rate of dispersion proportional to the product of the corresponding dispersion coefficient and concentration gradient. The principal factors governing dispersion in packed beds are discussed in a critical review by GUNN(26).

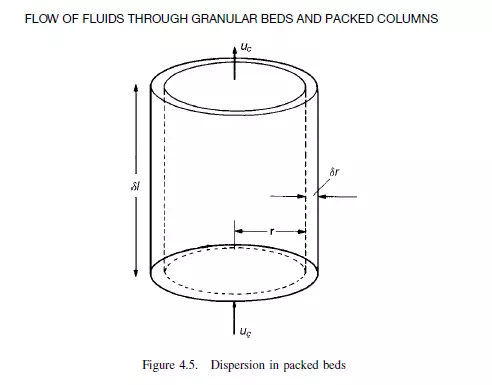
The differential equation for dispersion in a cylindrical bed of voidage e may be obtained by taking a material balance over an annular element of height δl, inner radius r,

and outer radius r + δr (as shown in Figure 4.5). On the basis of a dispersion model it is seen that if C is concentration of a reference material as a function of axial position l, radial position r, time t, and DL and DR are the axial and radial dispersion coefficients, then: Rate of entry of reference material due to flow in axial direction:

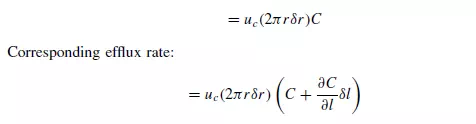
Longitudinal dispersion coefficients can be readily obtained by injecting a pulse of tracer into the bed in such a way that radial concentration gradients are eliminated, and measuring the change in shape of the pulse as it passes through the bed. Since ∂C/∂r is then zero, equation 4.34 becomes:

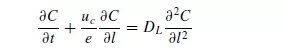
Values of DL can be calculated from the change in shape of a pulse of tracer as it passes between two locations in the bed, and a typical procedure is described by EDWARDS and RICHARDSON(27). GUNN and PRYCE(28), on the other hand, imparted a sinusoidal variation to the concentration of tracer in the gas introduced into the bed. The results obtained by a number of workers are shown in Figure 4.6 as a Peclet number Pe(= ucd/eDL) plotted against the particle Reynolds number (Re

_c= ucdρ/μ).For gases, at low Reynolds numbers (<1), the Peclet number increases linearly with Reynolds number, giving:

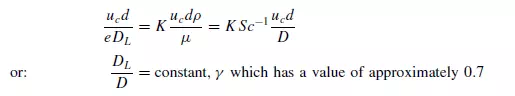
since Sc, the Schmidt number, is approximately constant for gases and the voidage of a randomly packed bed is usually about 0.4. This is consistent with the hypothesis that, at low Reynolds numbers, molecular diffusion predominates. The factor 0.7 is a tortuosity

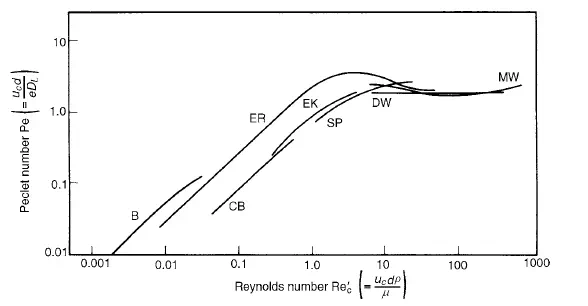
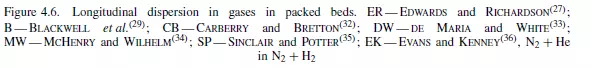
factor which allows for the fact that the molecules must negotiate a tortuous path because of the presence of the particles. At Reynolds numbers greater than about 10 the Peclet number becomes approximately constant, giving:

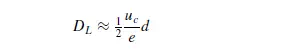
This equation is predicted by the mixing cell model, and turbulence theories put forward by ARIS and AMUNDSON(30) and by PRAUSNITZ(31). In the intermediate range of Reynolds numbers, the effects of molecular diffusivity and of macroscopic mixing are approximately additive, and the dispersion coefficient is given by an equation of the form:

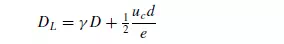
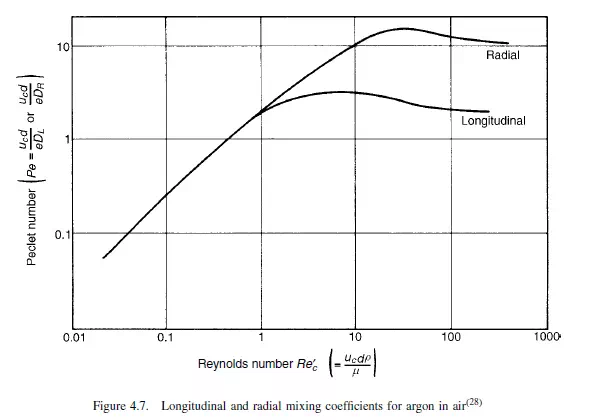
However, the two mechanisms interact and molecular diffusion can reduce the effects of convective dispersion. This can be explained by the fact that with streamline flow in a tube molecular diffusion will tend to smooth out the concentration profile arising from the velocity distribution over the cross-section. Similarly radial dispersion can give rise to lower values of longitudinal dispersion than predicted by equation 4.39. As a result the curves of Peclet versus Reynolds number tend to pass through a maximum as shown in Figure 4.6. A comparison of the effects of axial and radial mixing is seen in Figure 4.7, which shows results obtained by GUNN and PRYCE(28) for dispersion of argon into air. The values of DL were obtained as indicated earlier, and DR was determined by injecting a steady stream of tracer at the axis and measuring the radial concentration gradient across the bed. It is seen that molecular diffusion dominates at low Reynolds numbers, with both the axial and radial dispersion coefficients DL and DR equal to approximately 0.7 times the molecular diffusivity. At high Reynolds numbers, however, the ratio of the longitudinal dispersion coefficient to the radial dispersion coefficient approaches a value of about 5. That is:

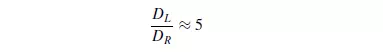
The experimental results for dispersion coefficients in gases show that they can be satisfactorily represented as Peclet number expressed as a function of particle Reynolds

number, and that similar correlations are obtained, irrespective of the gases used. However, it might be expected that the Schmidt number would be an important variable, but it is not possible to test this hypothesis with gases as the values of Schmidt number are all approximately the same and equal to about unity. With liquids, however, the Schmidt number is variable and it is generally about three orders of magnitude greater than for a gas. Results for longitudinal dispersion available in the literature, and plotted in Figure 4.8, show that over the range of Reynolds numbers studied (10−2 < Re _ c < 103) the Peclet number shows little variation and is of the order of unity. Comparison of these results with the corresponding ones for gases (shown in Figure 4.6) shows that the effect of molecular diffusion in liquids is insignificant at

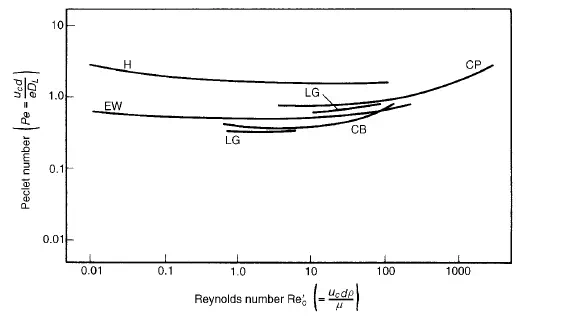
Reynolds numbers up to unity. This difference can be attributed to the very different magnitudes of the Schmidt numbers.