Under these conditions, from equation 3.5:

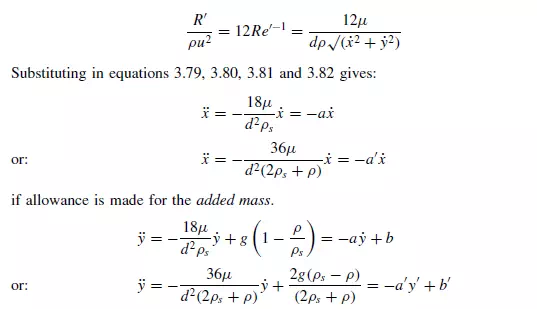
if allowance is made for the added mass. In this particular case, the equations of motion for the X and Y directions are mutually independent and therefore can be integrated separately. Furthermore, because the frictional term is now a linear function of velocity, the sign will automatically adjust to take account of whether motion is downwards or upwards. The equations are now integrated, ignoring the effects of added mass which can be accounted for by replacing a by a_ and b by b_. For the Y -direction, integrating equation 3.86 with respect to t :

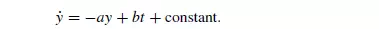
The axes are chosen so that the particle is at the origin at time t = 0. If the initial component of the velocity of the particle in the Y -direction is v, then, when t = 0, y = 0

and ˙y = v, and the constant = v,

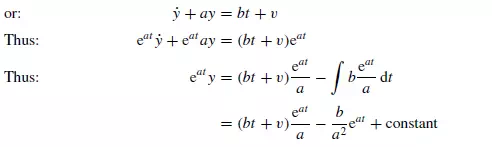
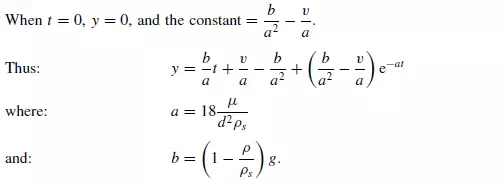
It may be noted that b/a = u0, the terminal falling velocity of the particle. This equation enables the displacement of the particle in the Y -direction to be calculated at any time t . For the X-direction, equation 3.84 is of the same form as equation 3.86 with b = 0. Substituting b = 0 and writing w as the initial velocity in the X-direction, equation 3.88 becomes:

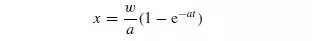
Thus the displacement in the X-direction may also be calculated for any time t . By eliminating t between equations 3.89, 3.90 and 3.91, a relation between the displacements in the X– and Y -directions is obtained. Equations of this form are useful for calculating the trajectories of particles in size-separation equipment. From equation 3.91: