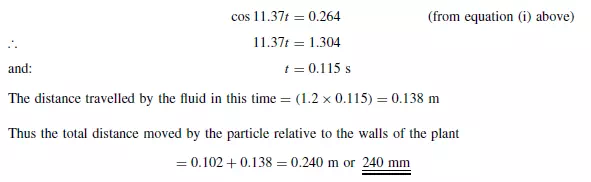For the Stokes’ law regime equations 3.88, 3.89 and 3.90 are applicable. For the Newton’s law regime, R_/ρu2 is a constant and equal to 0.22 for a spherical particle. Therefore, substituting in equation 3.81 and putting ˙x = 0 for vertical motion, and using the negative sign for downward motion (and neglecting the effect of added
mass):
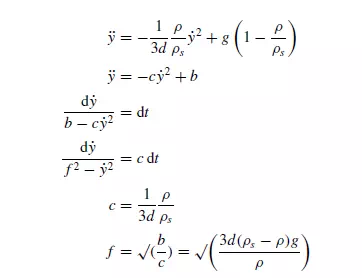




The relation between y and t may also be obtained graphically, though the process is more tedious than that of using the analytical solution appropriate to the particular case in question. When Re_ lies between 0.2 and 500 there is no analytical solution to the problem and a numerical or graphical method must be used. When the spherical particle is moving downwards, that is when its velocity is positive:

From these equations, Re_ may be obtained as a function of t . The velocity ˙y may then be calculated. By means of a second graphical integration, the displacement y may be
found at any time t . In using the various relations which have been obtained, it must be noted that the law of motion of the particle will change as the relative velocity between the particle and the fluid changes. If, for example, a particle is initially moving upwards with a velocity v, so that the corresponding value of Re _ is greater than about 500, the relation between y and t will be given by equation 3.104. The velocity of the particle will progressively decrease and, when Re_ is less than 500, the motion is obtained by application of equation 3.106. The upward velocity will then fall still further until Re _ falls below 0.2. While the particle is moving under these conditions, its velocity will fall to zero and will then gradually increase in the downward direction. The same equation (3.88) may be applied for the whole of the time the Reynolds group is less than 0.2, irrespective of sense. Then for higher downward velocities, the particle motion is given by equations 3.105 and 3.101. Unidimensional motion in the vertical direction, under the action of gravity, occurs frequently in elutriation and other size separation equipment, as described in Chapter 1.
Example
A material of density 2500 kg/m3 is fed to a size separation plant where the separating fluid is water rising with a velocity of 1.2 m/s. The upward vertical component of the velocity of the particles is 6 m/s. How far will an approximately spherical particle, 6 mm diameter, rise relative to the walls of the plant before it comes to rest relative to the fluid?
Solution
Initial velocity of particle relative to fluid, v = (6.0 − 1.2) = 4.8 m/s. Thus: Re_ = (6 × 10−3 × 4.8 × 1000)/(1 × 10−3)= 28,800 When the particle has been retarded to a velocity such that Re_ = 500, the minimum value for which equation 3.104 is applicable:˙y= (4.8 × 500)/28,800 = 0.083 m/s In this solution, the effect of added mass is not taken into account. Allowance may be made by adjustment of the values of the constants in the equations as indicated in Section 3.7.3.
When Re_ is greater than 500, the relation between the displacement of the particle y and the time t is:
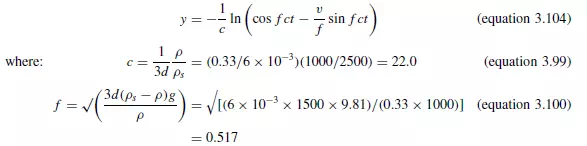



Thus whether the resistance force is calculated by equation 3.15 or equation 3.19, the particle moves a negligible distance with a velocity relative to the fluid of less than 0.083 m/s. Further, the time is also negligible, and thus the fluid also has moved through only a very small distance. It may therefore be taken that the particle moves through 0.102 m before it comes to rest in the fluid. The time taken for the particle to move this distance, on the assumption that the drag force corresponds to that given by equation 3.19, is given by: