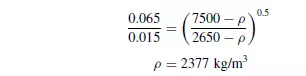Introduction

The problem of separating solid particles according to their physical properties is of great importance with large-scale operations in the mining industry, where it is necessary to separate the valuable constituents in a mineral from the adhering gangue, as it is called, which is usually of a lower density. In this case, it is first necessary to crush the material so that each individual particle contains only one constituent.  There is a similar problem in coal washing plants in which dirt is separated from the clean coal. The processing industries are more usually concerned with separating a single material, such as the product from a size reduction plant, into a number of size fractions, or in obtaining a uniform material for incorporation in a system in which a chemical reaction takes place. As similar problems are involved in separating a mixture into its constituents and into size fractions, the two processes are considered together. Separation depends on the selection of a process in which the behaviour of the material

is influenced to a very marked degree by some physical property. Thus, if a material is to be separated into various size fractions, a sieving method may be used because this

process depends primarily on the size of the particles, though other physical properties such as the shape of the particles and their tendency to agglomerate may also be involved. Other methods of separation depend on the differences in the behaviour of the particles in a moving fluid, and in this case the size and the density of the particles are the most important factors and shape is of secondary importance. Other processes make use of differences in electrical or magnetic properties of the materials or in their surface properties.

In general, large particles are separated into size fractions by means of screens, and small particles, which would clog the fine apertures of the screen or for which it would

be impracticable to make the openings sufficiently fine, are separated in a fluid. Fluid separation is commonly used for separating a mixture of two materials though magnetic, electrostatic and froth flotation methods are also used where appropriate. Considerable development has taken place into techniques for size separation in the

sub-sieve range. As discussed by WORK(27), the emphasis has been on techniques lending themselves to automatic working. Many of the methods of separation and much of the equipment has been developed for use in the mining and metallurgical industries, as described by TAGGART(28). Most processes which depend on differences in the behaviour of particles in a stream of fluid separate materials according to their terminal falling velocities, as reported in Chapter 3, which in turn depend primarily on density and size and to a lesser extent on shape. Thus, in many cases it is possible to use the method to separate a mixture of two materials into its constituents, or to separate a mixture of particles of the same material into a number of size fractions. If, for example, it is desired to separate particles of a relatively dense material A of

density ρA from particles of a less dense material B and the size range is large, the terminal falling velocities of the largest particles of B of density ρB may be greater than those of the smallest particles of A, and therefore a complete separation will not be possible. The maximum range of sizes that can be separated is calculated from the ratio of the sizes of the particles of the two materials which have the same terminal falling velocities. It is shown in Chapter 3 that this condition is given by equation 3.32 as:

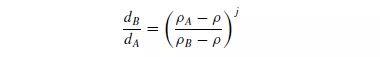
where j = 0.5 for fine particles, where Stokes’ law applies, and j = 1 for coarse particles where Newton’s law applies. It is seen that this size range becomes wider with increase in the density of the separating fluid and, when the fluid has the same density as the less dense material, complete separation is possible whatever the relative sizes. Although water is the most commonly used fluid, an effective specific gravity greater than unity is obtained if hindered settling takes place. Frequently, the fluid density is increased artificially by forming a suspension of small particles of a very dense solid, such as galena, ferro-silicon, magnetite, sand or clay, in the water. These suspensions have effective densities of up to about 3500 kg/m3. Alternatively, zinc chloride or calcium chloride solutions may be used. On the small scale, liquids with a range of densities are produced by mixing benzene and carbon tetrachloride. If the particles are allowed to settle in the fluid for only a very short time, they will not attain their terminal falling velocities and a better degree of separation can be obtained. A particle of material A will have an initial acceleration g[1 − (ρ/ρA)], because there is no fluid friction when the relative velocity is zero. Thus the initial velocity is a function of density only and it is unaffected by size and shape. A very small particle of the denser material will therefore always commence settling at a greater rate than a large particle of the less dense material. Theoretically, therefore, it should be possible to

separate materials completely, irrespective of the size range, provided that the periods of settling are sufficiently short. In practice, the required periods will often be so short that it is impossible to make use of this principle alone, although a better degree of separation may be obtained if the particles are not allowed to become fully accelerated. As the time of settling increases, the larger particles of the less dense material catch up and overtake the small heavy particles. Size separation equipment in which particles move in a fluid stream is now considered, noting that most of the plant utilises the difference in the terminal falling velocities of the particles: In the hydraulic jig, however, the particles are allowed to settle for only very brief periods at a time, and this equipment may therefore be used when the size range of the material is large.

Example

A mixture of quartz and galena of a size range from 0.015 mm to 0.065 mm is to be separated into two pure fractions using a hindered settling process. What is the minimum apparent density of the fluid that will give this separation? The density of galena is 7500 kg/m3 and the density of quartz is 2650 kg/m3.

Solution

Assuming the galena and quartz particles are of similar shapes, then from equation 1.42, the required density of fluid when Stokes’ law applies is given by: