A molecule is a group of atoms held together by chemical bonds. In quantum mechanical terms, a molecule is a group of particles consisting of at least two or more nuclei and one or more electrons. The molecule’s energy and other properties are calculated as expectation values of the molecule’s wavefunction, where the wavefunction is a function of the coordinates of all of the particles (nuclei + electrons) making up the molecule. The molecular wavefunction must satisfy all of the conditions that have been introduced so far, including an appropriate time-independent Schrödinger equation.
This page describes how to write “molecular” Schrödinger equations, and how to simplify these equations using the Born-Oppenheimer approximation and “atomic units”. The Hartree-Fock method for computing “model” molecular wavefunctions is also described briefly.
The “Molecular” Hamiltonian Operator
Molecules, assuming that they are not exchanging energy with their environment, must satisfy the time-independent Schrödinger equation:
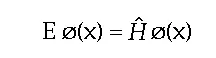

where ø is a function of the coordinates of ALL of the particles making up the molecule, x.
The Hamiltonian operator, H, is patterned after those discussed previously for the one electron “box” and atom. It contains a kinetic energy operator, T (i), for each particle in the molecule, and a potential energy operator, V (i,j), describing the Coulombic or electrical interaction between each pair of particles in the molecule:
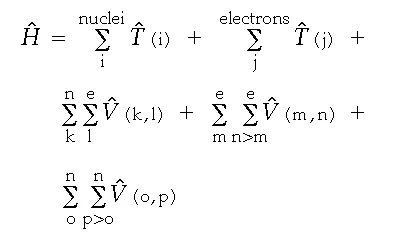
The operator contains five separate sums. The first contains a kinetic energy operator for each nucleus. The second contains a kinetic energy operator for each electron. The third contains a potential operator for each electron-nucleus pair, and the fourth and fifth contain a potential energy operator for each electron pair and each nucleus pair, respectively.
The definition of the individual T and V operators is straightforward. Namely,
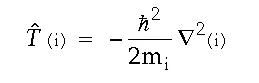

where “m” refers to the mass of particle “i” and the second derivatives are calculated with respect to the coordinates of particle “i”. Also,
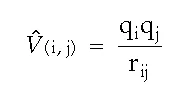

where “q” refers to the charge of a particle, and “r” is the distance between the two particles.
The above definitions show that the Hamiltonian operator depends in a simple and obvious way on a molecule’s composition. The operator is easily written down, but it is sufficiently complicated that exact algebraic solutions for ø can almost never be found (this result can be proven mathematically).
Born-Oppenheimer Approximation
Chemists routinely simplify the wavefunction problem by treating ø as a product of two wavefunctions – one that depends only on electron coordinates and one that depends only on nuclear coordinates. The justification for this is called the Born-Oppenheimer approximation.
The physical basis for separating electron motion from nuclear motion is the large difference in electron and nuclear masses (the lightest nucleus, a proton, is ~2000 times heavier than an electron). Electrons should normally move much faster than nuclei, and so we assume that electron behavior is always given by the best wavefunction for each nuclear geometry, i.e., we assume that the electrons adjust instantaneously to any change in nuclear geometry.
As a practical matter, this means that we specify a “nuclear” geometry for the molecule (hold the nuclei fixed), and then calculate a wavefunction and energy for the electrons. The sequence of steps is:
· select a nuclear geometry, i.e., specify the location of each nucleus;
· calculate an “electronic” wavefunction that describes electron behavior for this nuclear geometry, i.e., calculate the motion of the electrons relative to the nuclei;
· calculate the energy for this wavefunction (this gives the “electronic energy”);
· calculate the “potential” or “total” energy for the molecule by adding Vnn, the nuclear-nuclear interaction energy, to the electronic energy;
· if necessary, add the kinetic energy of the nuclei to the “total” energy
The electronic energy, Eelec, is obtained as an eigenvalue of the following “electronic” Schrödinger equation:
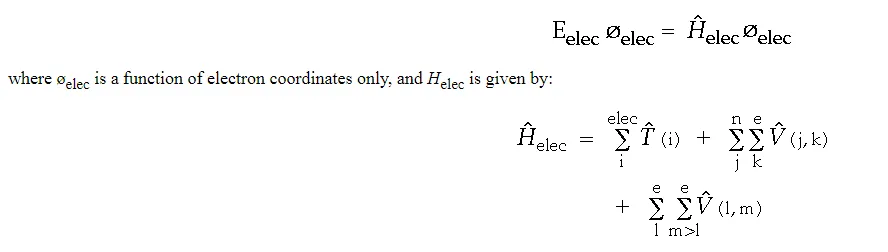
As a final simplification, we introduce the use of “atomic units”. In this unit system, the charge on an electron is -1, the charge on a proton is +1, the mass of an electron is 1, and  = 1.
= 1.
The electronic Hamiltonian can now be written as:
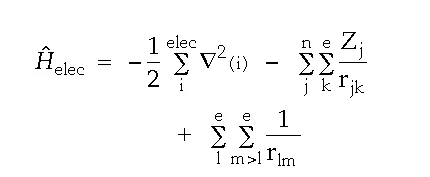

where Zj is the atomic number of nucleus “j” and “r” is the distance between the indicated particles.
The atomic units of energy (hartree) and distance (bohr) are especially important, and these are:
1 hartree = 627.51 kcal/mol = 27.21 eV
1 bohr = 0.529 Å
[Note: chemists often write “au” instead of “hartree” or “bohr”, especially when the type of unit, energy or distance, can be identified by context.]
Some interesting and useful facts about atomic units:
· The energy of a ground state (1s) hydrogen atom is exactly -0.5 au
· The interaction energy of an electron and a proton separated by 1 au is exactly -1 au
· From the virial theorem, Ven for the ground state hydrogen atom is exactly -1 au (i.e., twice the total energy).
· The most probable distance between an electron and a proton in the ground state hydrogen atom is 1 au
· The radius of the lowest energy electron orbit in the Bohr atom is 1 au
We cannot find algebraic wavefunction formulas that will satisfy even the “electronic” Schrödinger equation. Therefore, it is necessary to calculate “model” wavefunctions that closely simulate the electronic wavefunction. The most widely used method for constructing such models is the Hartree-Fock or HF method, and the following section describes the method qualitatively.
First, note that the electronic Hamiltonian contains three sums. Each term in the first two sums involves the coordinates of only a single electron, so these terms are called “one-electron” operators, h. Each term in the third sum involves the coordinates of only two electrons, so these terms are called “two-electron” operators, g. We can rewrite the electronic Hamiltonian, then, as:
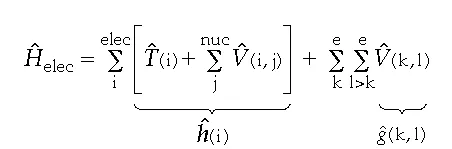

The two-electron operators are the main reason we cannot solve the Schrödinger equation algebraically, so let’s consider what could be accomplished if we ignored them. It is easy to show that if one has found “one-electron” wavefunctions, øi, that are eigenfunctions of h, i.e.,
h øi = ei øi
then Ø, a wavefunction that is a product of ø for each electron, will be an eigenfunction of Hone, where Hone is the sum of h. In other words, if
Ø = øa(1)øb(2)…øn(N)
then
HoneØ = EØ
where
E = ea + eb + … + en
(first part only; see eq. 6.4-6.6)
The most popular computational method, the Hartree-Fock (HF) method, adopts a similar strategy to construct model wavefunctions. Instead of h, the HF method uses an one-electron operator called the “Fock” operator, F. This operator contains h and an additional operator that describes the interaction between electron “i” and all of the other electrons as a function of the position of “i” only (this is accomplished by having “i” interact with the “average” positions of the other electrons rather than their actual positions). The one-electron wavefunctions, ø, that satisfy
F øi = ei øi
are called molecular orbitals, and the “ei” are called molecular orbital energies. The HF wavefunction, ØHF, is assembled from products of the molecular orbitals. Note, however, that the HF energy is not the sum of the orbital energies. EHF is calculated as the expectation value of Helec (we will explain why later).
Two additional important points:
Molecular orbitals must be calculated iteratively. We don’t know the “average” positions of the other electrons to begin with, so we have to guess their positions, use this guess to calculate ø, and then use ø to calculate the “average” positions. The new “average” positions are used to calculate new ø, and the process repeats over and over until ø no longer changes significantly. At this point, we say that a “self-consistent (electric) field” or SCF has been achieved.
Also, we cannot calculate the molecular orbitals algebraically. We must settle for “model” molecular orbitals. Thus, an actual HF calculation yields a model of an “ideal” HF wavefunction which is, in turn, a model of the exact wavefunction. Even so, the “model” HF wavefunction and energy can be quite useful.


Comments are closed