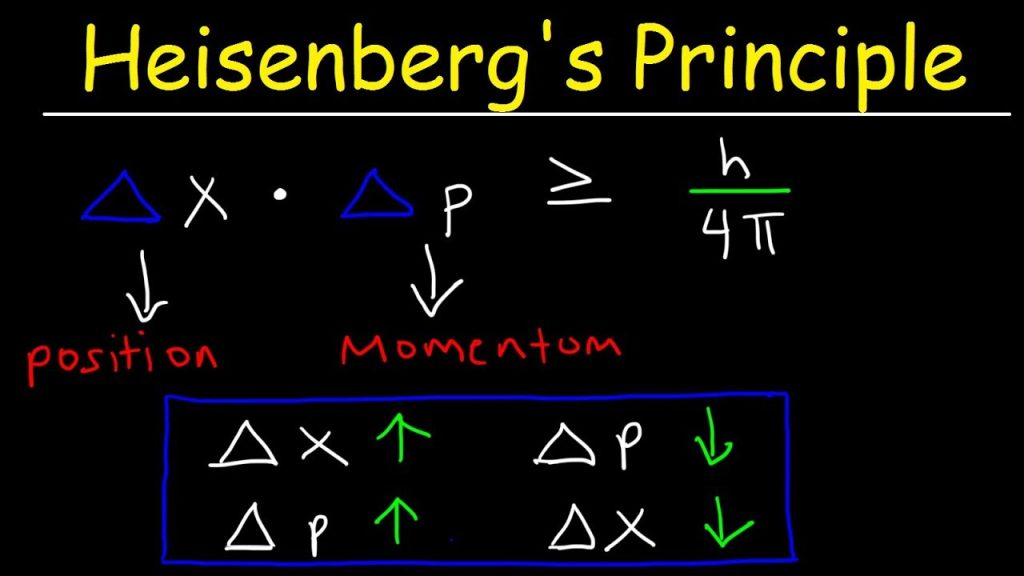
The Heisenberg uncertainty principle, stated in a way that’s useful for chemists, is that it’s impossible to determine simultaneously with high precision both the momentum and position of an electron.

In practice, this means the orbitals occupied by electrons cannot be calculated or drawn with high precision.

Orbitals are based on probability distributions for an electron.

For example: an orbital may be drawn under the condition that there is a 99% chance that at any given time an electron will be within its volume. The electron is elsewhere the rest of the time.

Typical orbitals are shown below:

Sublevel schematics: the 2s and 2p sublevels

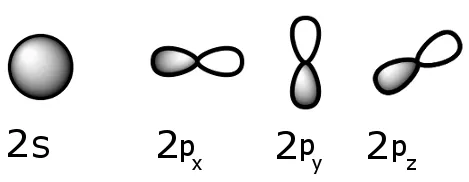
More broadly, the Heisenberg uncertainty principle applies to pairs of complementary variables. Position and momentum form one such pair, while energy and time form another. The uncertainty principle applies to objects of any mass but is significant only for extremely small objects such as atomic and subatomic particles.

Consider the question: What is the momentum, p, and position, x, of a particle at time t?

To know the position, the particle must be localized at x, with uncertainty of Δx. Therefore the de Broglie wave associated with it must also be localized. A localized wave is formed from a superposition of many waves of different wavelengths, but this implies many different values of momentum, because p=h/λ. (h is Planck’s constant and λ is wavelength.)

Therefore we cannot associate a definite momentum with such a localized particle and hence Δp is large.

If, on the other hand, momentum is definite, the de Broglie wave would have a wavelength spread out through space – i.e. non-localized and large Δx.

It can be shown that:

δpδx ≥ h/4π