The sedimentation of metallurgical slimes has been studied by COE and CLEVENGER(2), who concluded that a concentrated suspension may settle in one of two different ways.

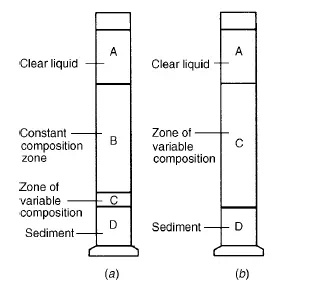
In the first, after an initial brief acceleration period, the interface between the clear liquid and the suspension moves downwards at a constant rate and a layer of sediment builds up at the bottom of the container. When this interface approaches the layer of sediment, its rate of fall decreases until the “critical settling point” is reached when a direct interface is formed between the sediment and the clear liquid. Further sedimentation then results solely from a consolidation of the sediment, with liquid being forced upwards around the solids which are then forming a loose bed with the particles in contact with one another. Since the flow area is gradually being reduced, the rate progressively diminishes. In Figure 5.1a, a stage in the sedimentation process is illustrated. A is clear liquid, B is suspension of the original concentration, C is a layer through which the concentration gradually increases, and D is sediment. The sedimentation rate remains constant until the upper interface corresponds with the top of zone C and it then falls until the critical settling point is reached when both zones B and C will have disappeared. A second and rather less common mode of sedimentation as shown in Figure 5.1b, is obtained when the range of particle size is very great. The sedimentation rate progressively decreases throughout the whole operation because there is no zone of constant composition, and zone C extends from the top interface to the layer of sediment. The main reasons for the modification of the settling rate of particles in a concentrated suspension are as follows:

a)    If a significant size range of particles is present, the large particles are settling relative to a suspension of smaller ones so that the effective density and viscosity

of the fluid are increased.

b)    The upward velocity of the fluid displaced during settling is appreciable in a concentrated suspension and the apparent settling velocity is less than the actual velocity

relative to the fluid.

c)     The velocity gradients in the fluid close to the particles are increased as a result of the change in the area and shape of the flow spaces.

d)    The smaller particles tend to be dragged downwards by the motion of the large particles and are therefore accelerated.

e)    Because the particles are closer together in a concentrated suspension, flocculation is more marked in an ionised solvent and the effective size of the small particles

is increased.

If the range of particle size is not more than about 6 : 1, a concentrated suspension settles with a sharp interface and all the particles fall at the same velocity. This is in

contrast with the behaviour of a dilute suspension, for which the rates of settling of the particles can be calculated by the methods given in Chapter 3, and where the settling

velocity is greater for the large particles. The two types of settling are often referred to as sludge line settling and selective settling respectively. The overall result is that in a

concentrated suspension the large particles are retarded and the small ones accelerated. Several attempts have been made to predict the apparent settling velocity of a concentrated suspension. In 1926 ROBINSON(3) suggested a modification of Stokes’ law and used the density (ρc) and viscosity (μc) of the suspension in place of the properties of the fluid to give:

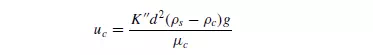
where K__ is a constant. The effective buoyancy force is readily calculated since:

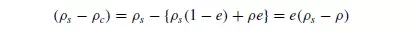
where e is the voidage of the suspension. Robinson determined the viscosity of the suspension μc experimentally, although it may be obtained approximately from the following formula of EINSTEIN(4):

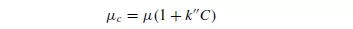
where: k__ is a constant for a given shape of particle (2.5 for spheres), C is the volumetric concentration of particles, and μ is the viscosity of the fluid.

This equation holds for values of C up to 0.02. For more concentrated suspensions, VAND(5) gives the equation:

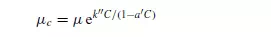
in which a_ is a second constant, equal to (39/64) = 0.609 for spheres. STEINOUR(6), who studied the sedimentation of small uniform particles, adopted a similar

approach, using the viscosity of the fluid, the density of the suspension and a function of the voidage of the suspension to take account of the character of the flow spaces, and obtained the following expression for the velocity of the particle relative to the fluid up:

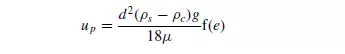
Since the fraction of the area available for flow of the displaced fluid is e, its upward velocity is uc(1 − e)/e so that:

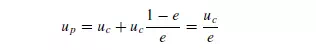
From his experiments on the sedimentation of tapioca in oil, Steinour found:

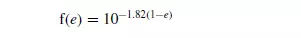
Substituting in equation 5.5, from equations 5.2, 5.6 and 5.7:

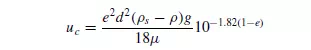
HAWKSLEY(7) also used a similar method and gave:

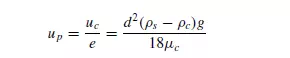
In each of these cases, it is correctly assumed that the upthrust acting on the particles is determined by the density of the suspension rather than that of the fluid. The use of an effective viscosity, however, is valid only for a large particle settling in a fine suspension. For the sedimentation of uniform particles the increased drag is attributable to a steepening of the velocity gradients rather than to a change in viscosity. The rate of sedimentation of a suspension of fine particles is difficult to predict because

of the large number of factors involved. Thus, for instance, the presence of an ionized solute in the liquid and the nature of the surface of the particles will affect the degree

of flocculation and hence the mean size and density of the flocs. The flocculation of a suspension is usually completed quite rapidly so that it is not possible to detect an

increase in the sedimentation rate in the early stages after the formation of the suspension. Most fine suspensions flocculate readily in tap water and it is generally necessary to add a deflocculating agent to maintain the particles individually dispersed. The factors involved in flocculation are discussed later in this chapter. A further factor influencing the sedimentation rate is the degree of agitation of the suspension. Gentle stirring may produce accelerated settling if the suspension behaves as a non-Newtonian fluid in which the apparent viscosity is a function of the rate of shear. The change in apparent viscosity can probably be attributed to the re-orientation of the particles. The effect of stirring is, however, most marked on the consolidation of the final sediment, in which “bridge formation” by the particles can be prevented by gentle stirring. During these final stages of consolidation of the sediment, liquid is being squeezed out through a bed of particles which are gradually becoming more tightly packed. A number of empirical equations have been obtained for the rate of sedimentation of suspensions, as a result of tests carried out in vertical tubes. For a given solid and liquid, the main factors which affect the process are the height of the suspension, the diameter of the containing vessel, and the volumetric concentration. An attempt at co-ordinating the results obtained under a variety of conditions has been made by WALLIS(8).