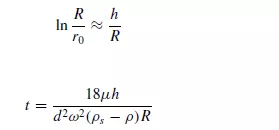In most practical cases where a particle is moving in a fluid under the action of a centrifugal field, gravitational effects are comparatively small and may be neglected. The
equation of motion for the particles is similar to that for motion in the gravitational field, except that the gravitational acceleration g must be replaced by the centrifugal acceleration rω2, where r is the radius of rotation and ω is the angular velocity. It may be noted, however, that in this case the acceleration is a function of the position r of the particle. For a spherical particle in a fluid, the equation of motion for the Stokes’ law region is:
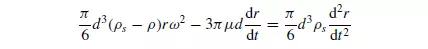
As the particle moves outwards, the accelerating force increases and therefore it never acquires an equilibrium velocity in the fluid. If the inertial terms on the right-hand side of equation 3.108 are neglected, then:
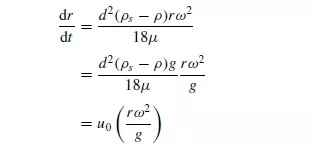
Thus, the instantaneous velocity (dr/dt) is equal to the terminal velocity u0 in the gravitational field, increased by a factor of rω2/g. Returning to the exact form (equation 3.108), this may be re-arranged to give:
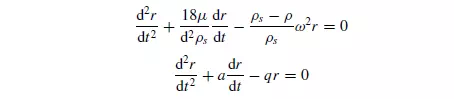
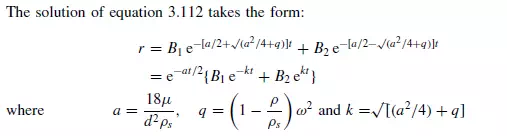
The effects of added mass, which have not been taken into account in these equations, require the replacement of a by a_ and q by q_, where:
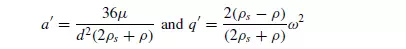
Equation 3.114 requires the specification of two boundary conditions in order that the constants B1 and B2 may be evaluated. If the particle starts (t = 0) at a radius r1 with zero velocity (dr/dt) = 0, then from equation 3.114:
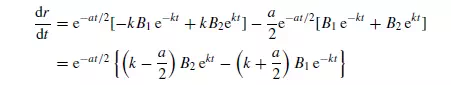
Substituting the boundary conditions into equations 3.114 and 3.116:
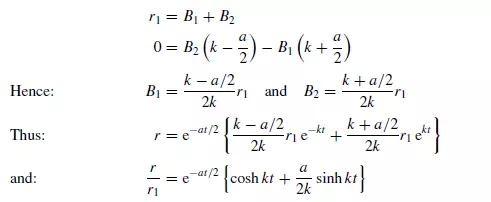
Hence r/r1 may be directly calculated at any value of t , although a numerical solution is required to determine t for any particular value of r/r1. If the effects of particle acceleration may be neglected, equation 3.112 simplifies to:
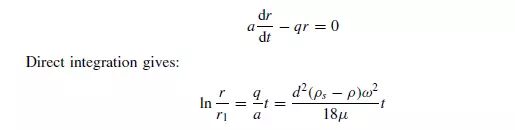
Thus the time taken for a particle to move to a radius r from an initial radius r1 is given by:
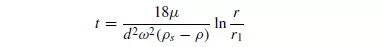
For a suspension fed to a centrifuge, the time taken for a particle initially situated in the liquid surface (r1 = r0) to reach the wall of the bowl (r = R) is given by:
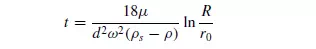
If h is the thickness of the liquid layer at the walls then:
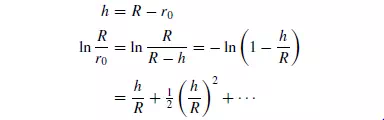
If h is small compared with R, then: