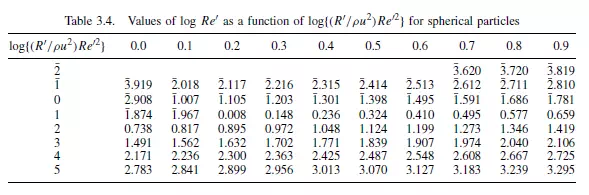
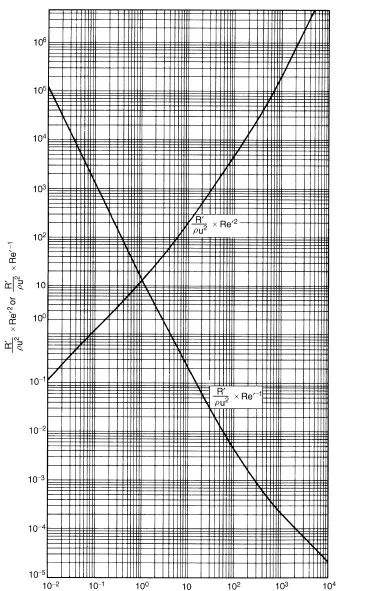
If a spherical particle is allowed to settle in a fluid under gravity, its velocity will increase until the accelerating force is exactly balanced by the resistance force. Although this state is approached exponentially, the effective acceleration period is generally of short duration for very small particles. If this terminal falling velocity is such that the corresponding  value of Re_ is less than 0.2, the drag force on the particle is given by equation 3.15. If the corresponding value of Re_ lies between 0.2 and 500, the drag force is given approximately by Schiller and Naumann in equation 3.17. It may be noted, however, that  if the particle has started from rest, the drag force is given by equation 3.15 until Re_exceeds 0.2. Again if the terminal falling velocity corresponds to a value of Re_ greater than about 500, the drag on the particle is given by equation 3.19. Under terminal falling conditions, velocities are rarely high enough for Re _ to approach 105, with the small particles generally used in industry.

The accelerating force due to gravity is given by:

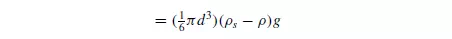
In the expressions given for the drag force and the terminal falling velocity, the following assumptions have been made:

a)     That the settling is not affected by the presence of other particles in the fluid. This condition is known as “free settling”. When the interference of other particles is

appreciable, the process is known as “hindered settling”.

b)     That the walls of the containing vessel do not exert an appreciable retarding effect.

c)      That the fluid can be considered as a continuous medium, that is the particle is large compared with the mean free path of the molecules of the fluid, otherwise the

              particles may occasionally “slip” between the molecules and thus attain a velocity higher than that calculated.

These factors are considered further in Sections 3.3.4 and 3.3.5 and in Chapter 5. From equations 3.24 and 3.25, it is seen that terminal falling velocity of a particle in

a given fluid becomes greater as both particle size and density are increased. If for a particle of material A of diameter dA and density ρA, Stokes’ law is applicable, then the

terminal falling velocity u0A is given by equation 3.24 as: