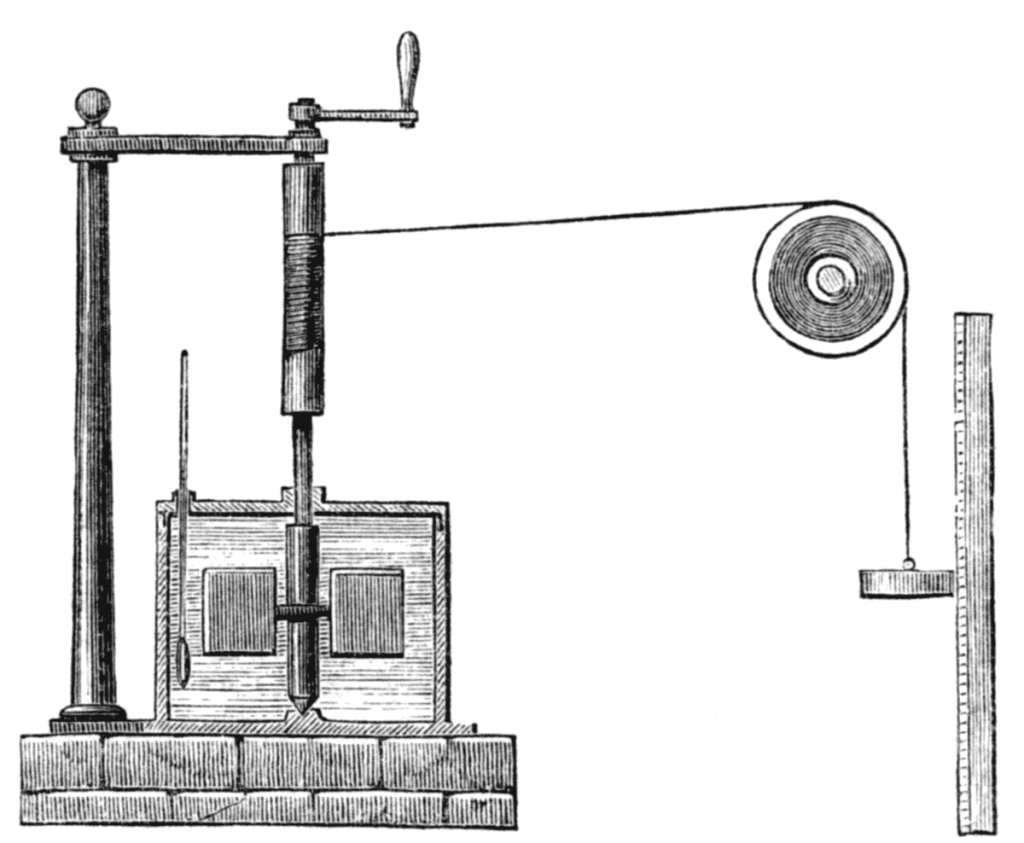
Two of the architects of modern thermodynamics were William Thompson (better known as Lord Kelvin) and his friend James Prescott Joule – a scientist of great vision, and a master of accurate thermodynamic measurement, as well as being something of an English eccentric. For example, while on a holiday in Switzerland in 1847, Thompson met Joule. Let Thompson describe what he saw: I was walking down from Chamonix to commence a tour of Mont Blanc, and whom should I meet walking up but Joule, with a long thermometer in his hand and a carriage with a lady in, not far off.
He told me that he had been married since we parted in Oxford [two weeks earlier] and that he was going to try for the elevation of temperature in waterfalls. Despite it being his honeymoon, Joule possessed a gigantic thermometer fully 4 to 5 feet in length (the reports vary). He spent much of his spare time during his honeymoon in making painstaking measurements of the temperature at the top and bottom of elongated Swiss waterfalls. He determined the temperature difference between the water at the bottom and top of the waterfall, finding it to be about 1 ◦ F warmer at the bottom.
In Joule’s own words, ‘A [water]fall of 817 feet [249 m] will generate one degree [Fahrenheit] of temperature’. This result is not attributable to colder air at the top of the waterfall, nor due to friction or viscous drag, or other effects occurring during the water’s descent, but is wholly due to a change in internal energy. The water was simply changing its altitude. The potential energy of a raised object is given by the expression.
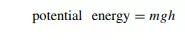
where m is the mass, g is the acceleration due to gravity and h the height by which it is raised. The potential energy of the water decreases during descent because its height decreases. This energy is liberated; and, as we have noted several times already, the simplest way to tell if the internal energy has increased is to determine its temperature. Joule showed the temperature of the water of the waterfalls had indeed increased. We could summarize by saying that thermodynamic work w is energetically equivalent to the lowering or raising of a weight (like the water of the waterfall, above), as discussed below.
Thermodynamic work
No one who has pumped up a bicycle tyre says it’s easy. Pumping a car tyre is harder still. It requires a lot of energy, and we really have to work at it. We saw in Chapter 1 how increasing the amount of a gas causes The pressure inside a party balloon is higher than the external, atmospheric pressure, as evidenced by the way it whizzes around a room when punctured. Work is a form of energy. The word ‘energy’ comes from the Greek en ergon, meaning ‘from work’. its volume to increase.
This increase in volume is needed to oppose any increases in pressure. It also explains why blowing into a party balloon causes it to get bigger. By contrast, a car tyre cannot expand greatly during pumping, so increasing the amount of gas it contains will increase its internal pressure. In a fully inflated car tyre, the internal pressure is about 10 times greater than ‘standard pressure’ p O , where p O has a value of 105 Pa. The first law of thermodynamics states that energy may be converted between forms, but cannot be created or destroyed. Joule was a superb experimentalist, and performed various types of work, each time generating energy in the form of heat.
In one set of experiments, for example, he rotated small paddles immersed in a water trough and noted the rise in temperature. This experiment was apparently performed publicly in St Anne’s Square, Manchester. Joule discerned a relationship between energy and work (symbol w). We have to perform thermodynamic work to increase the pressure within the tyre. Such work is performed every time a system alters its volume against an opposing pressure or force, or alters the pressure of a system housed within a constant volume.
Work and energy can be considered as interchangeable: we per- Work done on a system increases its energy, so U is positive. Work done by a system corresponds to a negative value of U. form work whenever energy powers a physical process, e.g. to propel a car or raise a spoon to the mouth. The work done on a system increases its energy, so the value of U increases, itself causing U to be positive). Work done by a system corresponds to a negative value of U.