The correct response is zero: For a particle at rest, or moving with constant velocity relative to an inertial frame, the resultant force acting on the isolated particle must be zero, must vanish. We usually attribute this to the unquestionable authority of Newton. The essential phrases in the question are constant velocity, resultant force and particle. Other words like “standing”, “elevator”, “ascending”, and “you” seem less important, even distracting, but they are there for a reason: The world that you as an engineer will analyze, re-design, and systematize is filled with people and elevators, not isolated particles, velocity vectors, or resultant forces — or at least, not at first sight. The latter concepts are abstractions which you must learn to identify in the world around you in order to work effectively as an engineer, e.g., in order to design an elevator.
The problems that appear in engineering text books are a kind of middle ground between abstract theory and everyday reality. We want you to learn to read and see through the superficial appearances, these descriptions which mask certain scientific concepts and principles, in order to grasp and appropriate the underlying forms that provide the basis for engineering analysis and design. The key phrase in Newton’s requirement is isolated particle: It is absolutely essential that you learn to abstract out of the problem statement and all of its relevant and irrelevant words and phrases, a vision of a particle as a point free in space. It’s best to render this vision, this abstraction “hard”by drawing it on a clean sheet of paper. Here is how it would look.

This is a non-trivial step, akin to a one month old’s apprehension that there are other egos in the world. You are to take the dot drawn as the representation of a thing, all things, that can be thought of as an isolated particle. Now show all the forces acting on the particle. We have the force due to gravity, W=Mg, acting vertically down, toward the center of the earth…. (Who said the elevator was oriented vertically? Who said it was on the surface of the earth? This information is not given; indeed, you could press the point, arguing that the question is not well posed. But is this information essential? We return to this point at the end of this chapter). We have the reaction force of the elevator floor acting vertically upward on you, on you as an abstraction, as an isolated particle. This is how our particle looks with all forces acting upon it. The resultant force is the vector sum of all the forces acting on the isolated particle. For static equilibrium of the isolated particle, the resultant of the two forces – W acting downward and R acting upward – must be zero.
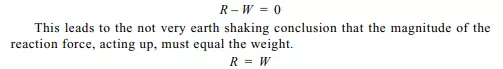
This apparently trivial result and simplicity of the problem, if indeed it can be called a problem, ought not to be allowed to deceive us: The introduction of the reaction of the floor on you, the passenger in the elevator, is characteristic of the most difficult step in applying the requirement of static equilibrium to an isolated particle. You will find it takes courage, as well as facility with the language of engineering mechanics, to venture forth and construct reaction forces out of thin air. They are there, hidden at the interface of your particle with the rest of the world. Some, like gravity, act at a distance, across all boundaries you may draw.