When elastic response under arbitrary deformation gradients is considered—because rotations, if not strains, are large or, in a material such as rubber, because the strains are large too—it is necessary to dispense with the infinitesimal strain theory. In such cases, the combined first and second laws of thermodynamics have the form ρ0θds + det[F]tr([F]−1[σ][dF]) = ρ0de, where [F]−1 is the matrix inverse of the deformation gradient [F]. If a parcel of material is deformed by [F] and then given some additional rigid rotation, the free energy f must be unchanged in that rotation. In terms of the polar decomposition [F] = [R][U], this is equivalent to saying that f is independent of the rotation part [R] of [F], which is then equivalent to saying that f is a function of the finite strain measure [EM] = (1/2)([F]T[F] − [I]) based on change of metric or, for that matter, on any member of the family of material strain tensors. Thus,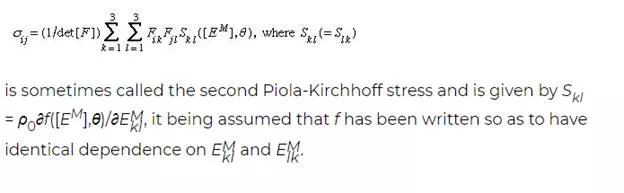
Inelastic response
The above mode of expressing [σ] in terms of [S] is valid for solids showing viscoelastic or plastic response as well, except that [S] is then to be regarded not only as a function of the present [EM] and θ but also as dependent on the prior history of both. Assuming that such materials show elastic response to sudden stress changes or to small unloading from a plastically deforming state, [S] may still be expressed as a derivative of f, as above, but the derivative is understood as being taken with respect to an elastic variation of strain and is to be taken at fixed θ and with fixed prior inelastic deformation and temperature history. Such dependence on history is sometimes represented as a dependence of f on internal state variables whose laws of evolution are part of the inelastic constitutive description. There are also simpler models of inelastic response, and the most commonly employed forms for plasticity and creep in isotropic solids are presented next.
To a good approximation, plastic deformation of crystalline solids causes no change in volume; and hydrostatic changes in stress, amounting to equal change of all normal stresses, have no effect on plastic flow, at least for changes that are of the same order or magnitude as the strength of the solid in shear. Thus, plastic response is usually formulated in terms of deviatoric stress, which is defined by τij = σij − δij(σ11 + σ22 + σ33)/3. Following Richard von Mises, in a procedure that is found to agree moderately well with experiment, the plastic flow relation is formulated in terms of the second invariant of deviatoric stress, commonly rewritten as

Thus, in the rate-independent plasticity version of the theory, tensile data (or compressive, with appropriate sign reversals) from a monotonic load test is assumed to define a function ε p(σ ). In the viscoplastic or high-temperature creep versions of the theory, tensile data is interpreted to define dε P/dt as a function of σ in the simplest case, representing, for example, secondary creep, and as a function of σ and ε p in theories intended to represent transient creep effects or rate-sensitive response at lower temperatures. Consider first the rigid-plastic material model in which elastic deformability is ignored altogether, as is sometimes appropriate for problems of large plastic flow, as in metal forming or long-term creep in the Earth’s mantle or for analysis of plastic collapse loads on structures. The rate of deformation tensor Dij is defined by 2Dij = ∂vi/∂xj + ∂vj/∂xi, and in the rigid-plastic case [D] can be equated to what may be considered its plastic part [Dp], given as D
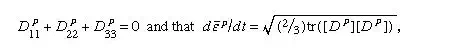
which must be integrated over previous history to get εp as required for viscoplastic models in which dεp/dt is a function of σ and εp. In the rate-independent version, [Dp] is defined as zero whenever σ is less than the highest value that it has attained in the previous history or when the current value of σ is the highest value but dσ/dt < 0. (In the elastic-plastic context, this means that “unloading” involves only elastic response.) For the ideally plastic solid, which is idealized to be able to flow without increase of stress when σ equals the yield strength level, dεp/dt is regarded as an undetermined but necessarily nonnegative parameter, which can be determined (sometimes not uniquely) only through the complete solution of a solid mechanics boundary-value problem.