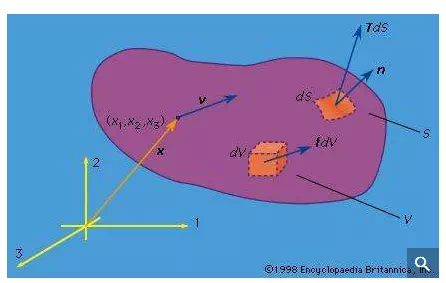
Let x denote the position vector of a point in space as measured relative to the origin of a Newtonian reference frame; x has the components (x1, x2, x3) relative to a Cartesian set of axes, which is fixed in the reference frame and denoted as the 1, 2, and 3 axes in Figure 1. Suppose that a material occupies the part of space considered, and let v = v(x, t) be the velocity vector of the material point that occupies position x at time t; that same material point will be at position x + vdt an infinitesimal interval dt later. Let ρ = ρ(x, t) be the mass density of the material. Here v and ρ are macroscopic variables. What is idealized in the continuum model as a material point, moving as a smooth function of time, will correspond on molecular-length (or larger but still “microscopic”) scales to a region with strong fluctuations of density and velocity. In terms of phenomena at such scales, ρ corresponds to an average of mass per unit of volume, and ρv to an average of linear momentum per unit volume, as taken over spatial and temporal scales that are large compared to those of the microscale processes but still small compared to those of the intended application or phenomenon under study. Thus, from the microscopic viewpoint, v of the continuum theory is a mass-weighted average velocity.

The linear momentum P and angular momentum H (relative to the coordinate origin) of the matter instantaneously occupying any volume V of space are then given by summing up the linear and angular momentum vectors of each element of material. Such summation over infinitesimal elements is represented mathematically by the integrals P = ∫V ρvdV and H = ∫V ρx × vdV. In this discussion attention is limited to situations in which relativistic effects can be ignored. Let F denote the total force and M the total torque, or moment (relative to the coordinate origin), acting instantaneously on the material occupying any arbitrary volume V. The basic laws of Newtonian mechanics are the linear and angular momentum principles that F = dP/dt and M = dH/dt, where time derivatives of P and H are calculated following the motion of the matter that occupies V at time t. When either F or M vanishes, these equations of motion correspond to conservation of linear or angular momentum.

An important, very common, and nontrivial class of problems in solid mechanics involves determining the deformed and stressed configuration of solids or structures that are in static equilibrium; in that case the relevant basic equations are F = 0 and M = 0. The understanding of such conditions for equilibrium, at least in a rudimentary form, long predates Newton. Indeed, Archimedes of Syracuse (3rd century BC), the great Greek mathematician and arguably the first theoretically and experimentally minded physical scientist, understood these equations at least in a nonvectorial form appropriate for systems of parallel forces. This is shown by his treatment of the hydrostatic equilibrium of a partially submerged body and by his establishment of the principle of the lever (torques about the fulcrum sum to zero) and the concept of centre of gravity.