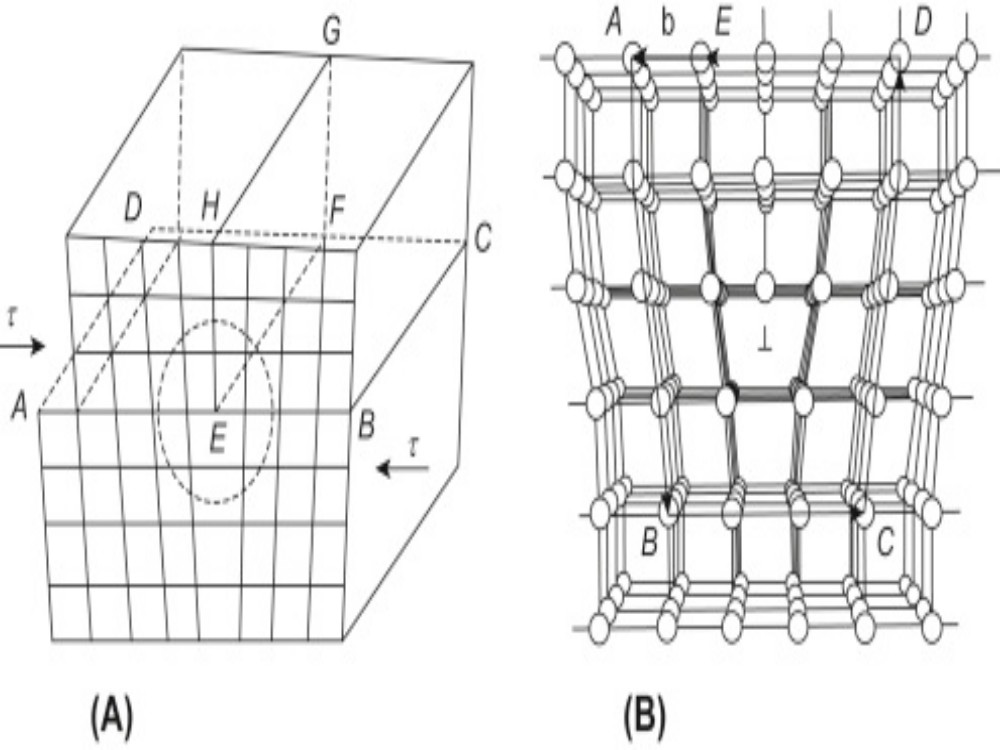
The Italian elastician and mathematician Vito Volterra introduced in 1905 the theory of the elastostatic stress and displacement fields created by dislocating solids. This involves making a cut in a solid, displacing its surfaces relative to one another by some fixed amount, and joining the sides of the cut back together, filling in with material as necessary. The initial status of this work was simply regarded as an interesting way of generating elastic fields, but, in the early 1930s, Geoffrey Ingram Taylor, Egon Orowan, and Michael Polanyi realized that just such a process could be going on in ductile crystals and could provide an explanation of the low plastic shear strength of typical ductile solids, much as Griffith’s cracks explained low fracture strength under tension. In this case, the displacement on the dislocated surface corresponds to one atomic lattice spacing in the crystal. It quickly became clear that this concept provided the correct microscopic description of metal plasticity, and, starting with Taylor in the 1930s and continuing into the 1990s, the use of solid mechanics to explore dislocation interactions and the microscopic basis of plastic flow in crystalline materials has been a major topic, with many distinguished contributors.
The mathematical techniques advanced by Volterra are now in common use by earth scientists in explaining ground displacement and deformation induced by tectonic faulting. Also, the first elastodynamic solutions for the rapid motion of crystal dislocations, developed by South African materials scientist F.R.N. Nabarro in the early 1950s, were quickly adapted by seismologists to explain the radiation from propagating slip distributions on faults. The Japanese seismologist H. Nakano had already shown in 1923 how to represent the distant waves radiated by an earthquake as the elastodynamic response to a pair of force dipoles amounting to zero net torque. (All his manuscripts were destroyed in the fire in Tokyo associated with the great Kwanto earthquake in that same year, but copies of some had been sent to Western colleagues and the work survived.)
Continuum plasticity theory
The macroscopic theory of plastic flow has a history nearly as old as that of elasticity. While in the microscopic theory of materials, the word “plasticity” is usually interpreted as denoting deformation by dislocation processes, in macroscopic continuum mechanics it is taken to denote any type of permanent deformation of materials, especially those of a type for which time or rate of deformation effects are not the most dominant feature of the phenomenon (the terms viscoplasticity, creep, or viscoelasticity are usually used in such cases). Coulomb’s work of 1773 on the frictional yielding of soils under shear and normal stress has been mentioned; yielding denotes the occurrence of large shear deformations without significant increase in applied stress. His results were used to explain the pressure of soils against retaining walls and footings in the work of the French mathematician and engineer Jean Victor Poncelet in 1840 and the Scottish engineer and physicist William John Macquorn Rankine in 1853. The inelastic deformation of soils and rocks often takes place in situations for which the deforming mass is infiltrated by groundwater, and Austrian-American civil engineer Karl Terzaghi in the 1920s developed the concept of effective stress, whereby the stresses that enter a criterion of yielding or failure are not the total stresses applied to the saturated soil or rock mass but rather the effective stresses, which are the difference between the total stresses and those of a purely hydrostatic stress state with pressure equal to that in the pore fluid. Terzaghi also introduced the concept of consolidation, in which the compression of a fluid-saturated soil can take place only as the fluid slowly flows through the pore space under pressure gradients, according to Darcy’s law; this effect accounts for the time-dependent settlement of constructions over clay soils.
Apart from the earlier observation of plastic flow at large stresses in the tensile testing of bars, the theory of continuum plasticity for metallic materials begins with Henri Edouard Tresca in 1864. His experiments on the compression and indentation of metals led him to propose that this type of plasticity, in contrast to that in soils, was essentially independent of the average normal stress in the material and dependent only on shear stresses, a feature later rationalized by the dislocation mechanism. Tresca proposed a yield criterion for macroscopically isotropic metal polycrystals based on the maximum shear stress in the material, and that was used by Saint-Venant to solve an early elastic-plastic problem, that of the partly plastic cylinder in torsion, and also to solve for the stresses in a completely plastic tube under pressure.
The German applied mechanician Ludwig Prandtl developed the rudiments of the theory of plane plastic flow in 1920 and 1921, with an analysis of indentation of a ductile solid by a flat-ended rigid indenter, and the resulting theory of plastic slip lines was completed by H. Hencky in 1923 and Hilda Geiringer in 1930. Additional developments include the methods of plastic limit analysis, which allowed engineers to directly calculate upper and lower bounds to the plastic collapse loads of structures or to forces required in metal forming. Those methods developed gradually over the early 1900s on a largely intuitive basis, first for simple beam structures and later for plates, and were put on a rigorous basis within the rapidly developing mathematical theory of plasticity about 1950 by Daniel C. Drucker and William Prager in the United States and Rodney Hill in Great Britain.
The Austrian-American applied mathematician Richard von Mises proposed in 1913 that a mathematically simpler theory of plasticity than that based on the Tresca yield criterion could be based on the second tensor invariant of the deviatoric stresses (i.e., of the total stresses minus those of a hydrostatic state in which pressure is equal to the average normal stress over all planes). An equivalent yield criterion had been proposed independently by the Polish engineer Maksymilian Tytus Huber. The Mises theory incorporates a proposal by M. Levy in 1871 that components of the plastic strain increment tensor are in proportion to one another just as are the components of deviatoric stress. This criterion was generally found to provide slightly better agreement with experiment than did that of Tresca, and most work on the application of plasticity theory uses this form. Following a suggestion of Prandtl, E. Reuss completed the theory in 1930 by adding an elastic component of strain increments, related to stress increments in the same way as for linear elastic response. This formulation was soon generalized to include strain hardening, whereby the value of the second invariant for continued yielding increases with ongoing plastic deformation, and was extended to high-temperature creep response in metals or other hot solids by assuming that the second invariant of the plastic (now generally called “creep”) strain rate is a function of that same invariant of the deviatoric stress, typically a power law type with Arrhenius temperature dependence.
This formulation of plastic and viscoplastic, or creep, response has been applied to all manner of problems in materials and structural technology and in flow of geologic masses. Representative problems addressed include the growth and subsequent coalescence of microscopic voids in the ductile fracture of metals, the theory of the indentation hardness test, the extrusion of metal rods and rolling of metal sheets, design against collapse of ductile steel structures, estimation of the thickness of the Greenland Ice Sheet, and modeling the geologic evolution of the Plateau of Tibet. Other types of elastic-plastic theories intended for analysis of ductile single crystals originate from the work of G.I. Taylor and Hill and base the criterion for yielding on E. Schmid’s concept from the 1920s of a critical resolved shear stress along a crystal slip plane, in the direction of an allowed slip on that plane; this sort of yield condition has approximate support from the dislocation theory of plasticity.