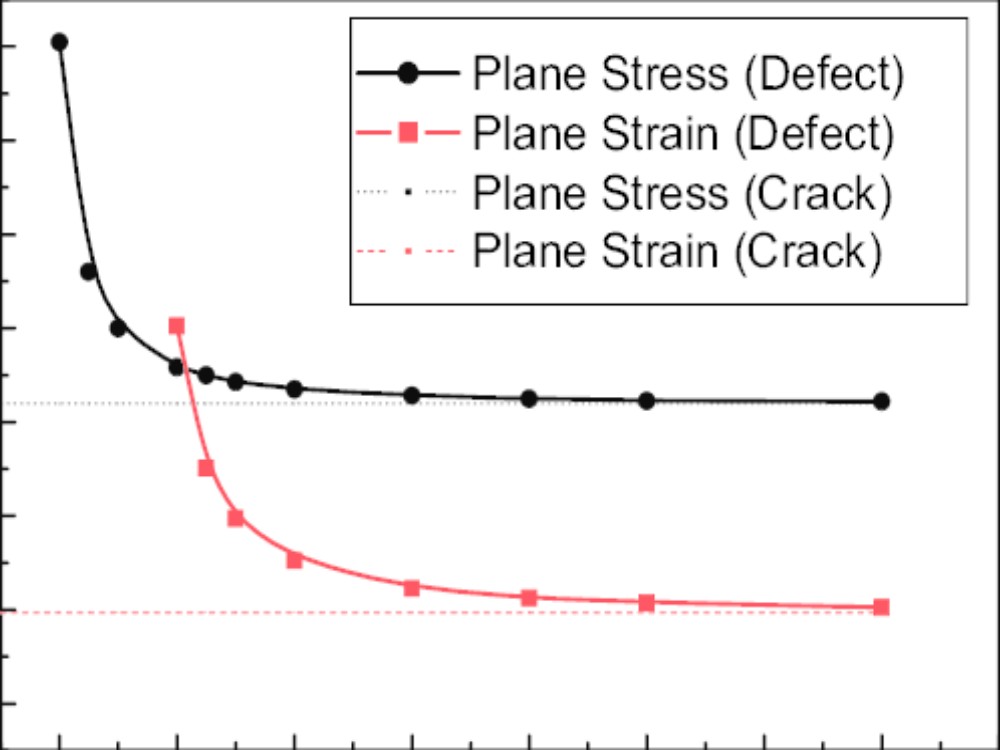
In 1898 G. Kirsch derived the solution for the stress distribution around a circular hole in a much larger plate under remotely uniform tensile stress. The same solution can be adapted to the tunnellike cylindrical cavity of a circular section in a bulk solid. Kirsch’s solution showed a significant concentration of stress at the boundary, by a factor of three when the remote stress was uniaxial tension. Then in 1907 the Russian mathematician Gury Vasilyevich Kolosov, and independently in 1914 the British engineer Charles Edward Inglis, derived the analogous solution for stresses around an elliptical hole. Their solution showed that the concentration of stress could become far greater, as the radius of curvature at an end of the hole becomes small compared with the overall length of the hole. These results provided the insight to sensitize engineers to the possibility of dangerous stress concentrations at sharp reentrant corners, notches, cutouts, keyways, screw threads, and similar openings in structures for which the nominal stresses were at otherwise safe levels. Such stress concentration sites are places from which a crack can nucleate.

The elliptical hole of Kolosov and Inglis defines a crack in the limit when one semimajor axis goes to zero, and the Inglis solution was adopted by the British aeronautical engineer A.A. Griffith in 1921 to describe a crack in a brittle solid. In that work Griffith made his famous proposition that a spontaneous crack growth would occur when the energy released from the elastic field just balanced the work required to separate surfaces in the solid. Following a hesitant beginning, in which Griffith’s work was initially regarded as important only for very brittle solids such as glass, there developed, largely under the impetus of the American engineer and physicist George R. Irwin, a major body of work on the mechanics of crack growth and fracture, including fracture by fatigue and stress corrosion cracking, starting in the late 1940s and continuing into the 1990s. This was driven initially by the cracking of a number of American Liberty ships during World War II, by the failures of the British Comet airplane, and by a host of reliability and safety issues arising in aerospace and nuclear reactor technology. The new complexion of the subject extended beyond the Griffith energy theory and, in its simplest and most widely employed version in engineering practice, used Irwin’s stress intensity factor as the basis for predicting crack growth response under service loadings in terms of laboratory data that is correlated in terms of that factor. That stress intensity factor is the coefficient of a characteristic singularity in the linear elastic solution for the stress field near a crack tip; it is recognized as providing a proper characterization of crack tip stressing in many cases, even though the linear elastic solution must be wrong in detail near the crack tip owing to nonelastic material response, large strain, and discreteness of material microstructure.