The general energy balance derived previously can be recast into a “mechanical energy balance.” The mechanical energy balance is most useful for processes in which changes in the potential and kinetic energies are of primary interest, rather than changes in internal energy or heat associated with the process. Thus the mechanical energy balance is mainly used for purely-mechanical flow problems – i.e. problems in which heat transfer, chemical reactions, or phase changes are not present. We start from equation 12, in which we have reverted from specific enthalpy notation back to internal energy and PV work using H j ˆ = U j ˆ + PjVj ˆ ,
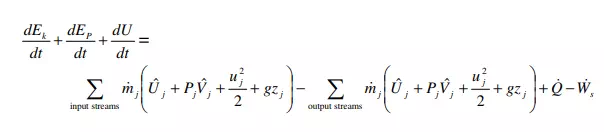
Now we make several additional assumptions. First, we assume steady state, so that all terms on the left hand side become zero. Second, we assume that the system has only a single inlet and a single outlet. Moreover, steady state implies that the inlet mass flowrate must equal the outlet mass flowrate, in order to avoid accumulation of material in the system. These adjustments lead to
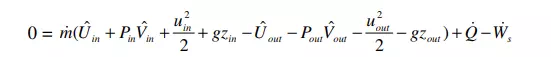
In the above equation, subscript “in” refers to the inlet port, and subscript “out” to the outlet port. Next, we divide the entire equation by m& , and write specific volume (volume/mass) as Vˆ = 1/ρ, where ρ is the density (mass/volume) of the flowing material. Moreover, we assume that the flow is incompressible, so that density is constant. A constant density means that Vˆ in = Vˆ out = 1/ρ. Also, we define ∆Uˆ = Uˆ out – Uˆ in, ∆P = Pout – Pin, etc. With these changes, equation 14 becomes
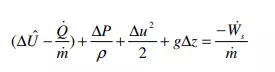
The term ( U Q m& ) & ∆ ˆ − – in the absence of chemical reactions, phase changes, or other sources of large amounts of heat transfer; i.e. under typical conditions of usage for the mechanical balance equation – will mostly represent heat generated due to the viscous friction in the fluid. In such situations, this term is called the friction loss and we will write it as Fˆ . With this last change, equation 15 assumes the usual form of the mechanical energy balance,
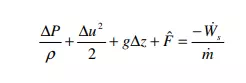
Note that m Ws & & is the shaft work performed by the system on the surroundings, per unit mass of material passing through the system.
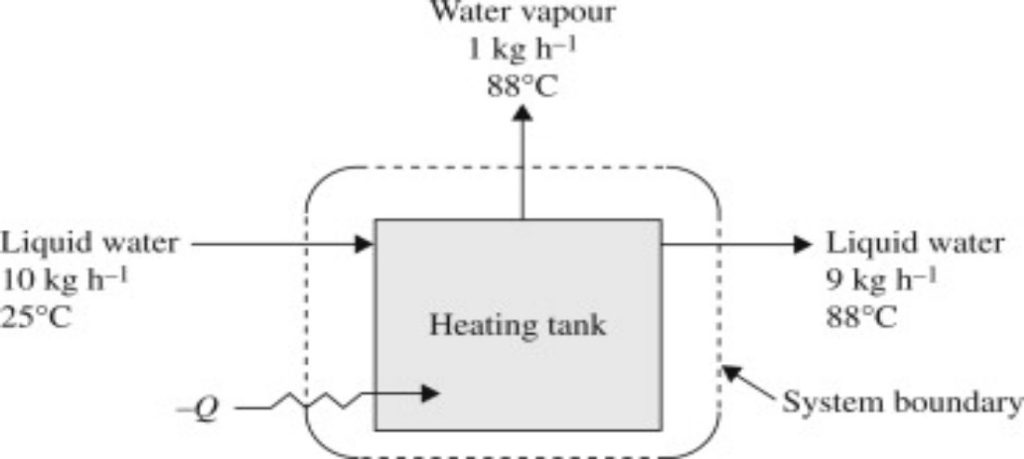
Comments are closed