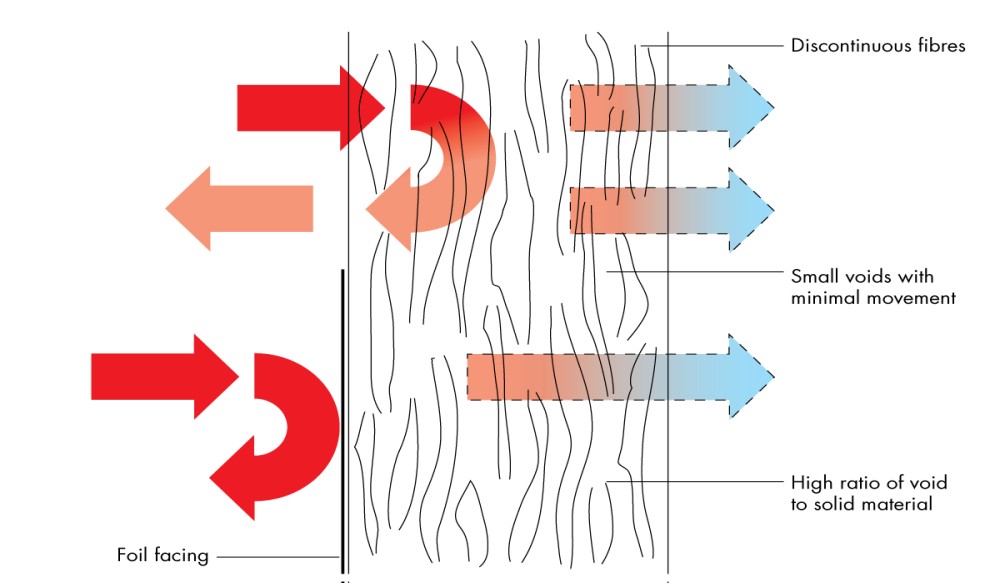
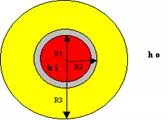
 The most basic model for insulation on a pipe is shown above. R1 and R2 show the inside and outside radius of the pipe respectively. R3 shows the radius of the insulation. Typically, when dealing with insulations, engineers must be concerned with linear heat loss or heat loss per unit length.
The most basic model for insulation on a pipe is shown above. R1 and R2 show the inside and outside radius of the pipe respectively. R3 shows the radius of the insulation. Typically, when dealing with insulations, engineers must be concerned with linear heat loss or heat loss per unit length.
Generally, the heat transfer coefficient of ambient air is 40 W/m2K. This coefficient can of course increase with wind velocity if the pipe is outside. A good estimate for an outdoor air coefficient in warm climates with wind speeds under 15 mph is around 50 W/m2K.
| Eq. (1) |
The total heat loss per unit length is calculated by:
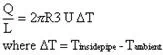 | Eq. (2) |
 |
| Figure 3: Heat Loss vs. InsulationThickness |
Since heat loss through insulation is a conductive heat transfer, there are instances when adding insulation actuallyincreases heat loss. The thickness at which insulation begins to decrease heat loss is described as the critical thickness. Since the critical thickness is almost always a few millimeters, it is seldom (if ever) an issue for piping. Critical thickness is a concern however in insulating wires. Figure 3 shows the heat loss vs. insulation thickness for a typical insulation. It’s easy to see why wire insulation is kept to a minimum as adding insulation would increase the heat transfer.