The key idea is that the energy created by the centrifugal force iskinetic energy. The amount of energy given to the liquid is proportional to the velocity at the edge or vane tip of the impeller. The faster the impeller revolves or the bigger the impeller is, then the higher will be the velocity of the liquid at the vane tip and the greater the energy imparted to the liquid.

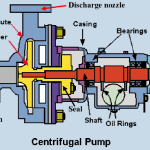
This kinetic energy of a liquid coming out of an impeller is harnessed by creating a resistance to the flow. The first resistance is created by the pump volute (casing) that catches the liquid and slows it down. In the discharge nozzle, the liquid further decelerates and its velocity is converted to pressure according to Bernoulli’s principle.

Therefore, the head (pressure in terms of height of liquid) developed is approximately equal to the velocity energy at the periphery of the impeller expressed by the following well-known formula:

Description: centpumps_eq1a

where:

H = Total Head developed in feet

v = Velocity at periphery of impleller in ft/s

g = Acceleration due to gravity = 32.2 ft/s2

Eq. 1

A handy formula for peripheral velocity is:

Description: centpumps_eq2a

where:

v = Velocity at periphery of impleller in ft/s

N = Impeller RPM (revolutions per minute)

D = Impeller diameter in inches

Eq. 2

This head can also be calculated from the readings on the pressure gauges attached to the suction and discharge lines.

One fact that must always be remembered: A pump does not create pressure, it only provides flow.

Pressure is a just an indication of the amount of resistance to flow.

Pump curves relate flow rate and pressure (head) developed by the pump at different impeller sizes and rotational speeds. The centrifugal pump operation should conform to the pump curves supplied by the manufacturer. In order to read and understand the pump curves, it is very important to develop a clear understanding of the terms used in the curves. This topic will be covered later.