The most simple form of distillation, called simple distillation, is a process in which a muticomponent liquid mixture is slowly boiled in an open pot and the vapors are continuously removed as they form. At any instant in time the vapor is in equilibrium with the
liquid remaining on the still. Because the vapor is always richer in the more volatile components than the liquid, the liquid composition changes continuously with time, becoming more and more concentrated in the least volatile species. A simpledistillation residue curve is a graph showing how the composition of the liquid residue curves on the pot changes over time. Aresidue curve map is a collection of the liquid residue curves originating from different initial compositions. Residue curve maps contain the same information as phase diagrams, but represent this information in a way that is more useful for understanding how to synthesize a distillation sequence to separate a mixture.
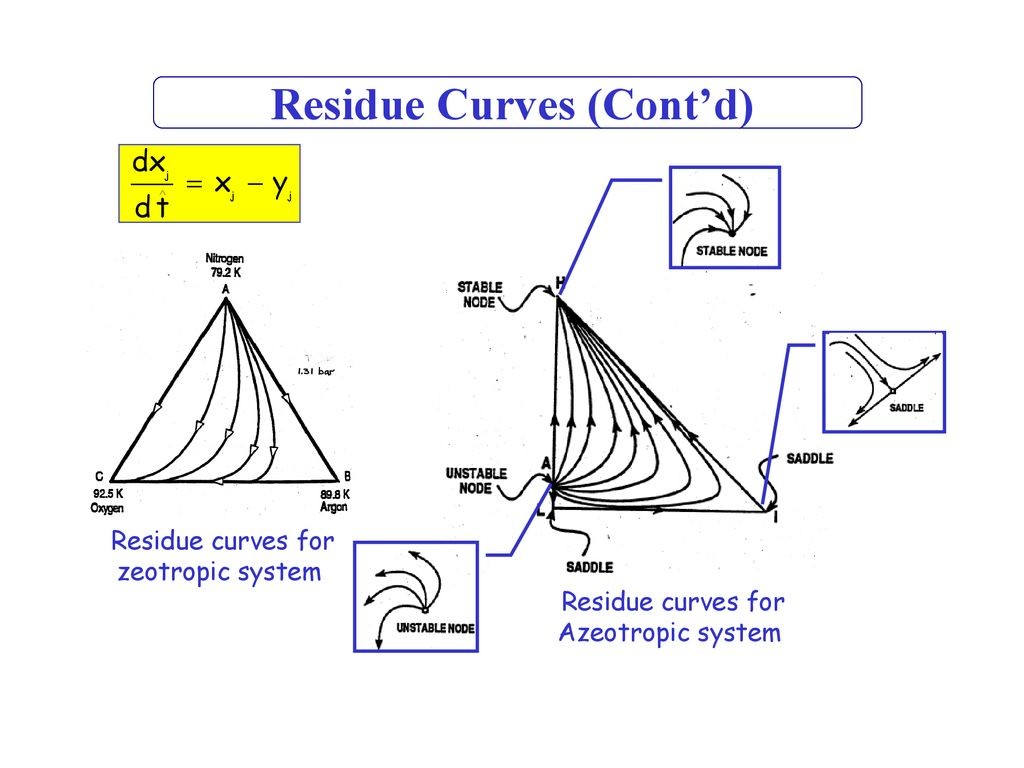
All of the residue curves originate at the light (lowest boiling) pure component in a region, move towards the intermediate boiling component, and end at the heavy (highest boiling) pure component in the same region. The lowest temperature nodes are termed as unstable nodes (UN), as all trajectories leave from them; while the highest temperature points in the region are termed stable nodes (SN), as all trajectories ultimately reach them. The point that the trajectories approach from one direction and end in a different direction (as always is the point of intermediate boiling component) are termed saddle point (S). Residue curve that divide the composition space into different distillation regions are called distillation boundaries. A better understanding of the residue curve map may be view in Figure 1. Â Notice that the trajectories move from the lowest temperature component towards the highest.
 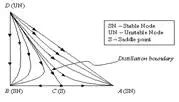 |
| Figure 1: Residue curve map for a ternary mixture with adistillation boundary running from pure component D tothe binary azeotrope C. |
Residue curve maps would be of limited usefulness if they could only be generated experimentally. Fortunately that is not the case. Using various references, the simple distillation process can be described by the set of equations:
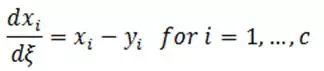 | Eq. (3) |
 where:
yi = mole fraction of component i in vapor phase
xi = mole fraction of component i in liquid phase
ξ = nonlinear time scale
c = number of component in the mixture
Research studies have also been done to determine the relationship between the number of nodes (stable and unstable) and saddle points one can have in a legitimately drawn ternary residue plot. The equation is based on topological arguments. One form for this equation is:
| 4(N3 – S3) + 2(N2 – S2) + (N1 – S1) = 1 | Eq. (4) |
where:
Ni = number of nodes (stable and unstable) involving i species
Si = number of saddles involving i species
Many different residue curve maps are possible when azeotropes are present. Ternary mixtures containing only one azeotrope may exhibit six possible residue curve maps that differ by the binary pair forming the azeotrope and by whether the azeotrope is minimum or maximum boiling.
Even though the simple distillation process has no practical use as a method for separating mixtures, simple distillation residue curve maps have extremely useful applications, such as:
1. Testing of the consistency of experimental azeotropic data;
2. Predict the order and content of the cuts in batch distillation;
3. In distillation, to check whether the given mixture is separable by distillation, identification of the entrainers / solvents, prediction of attainable product compositions, qualitative prediction of composition profile shape, and synthesis of the corresponding distillation column.
By identifying the limiting separation achievable by distillation, residue curve maps are also useful in synthesizing separation sequences combining distillation with other methods.