An electron tube has two or more electrodes separated either by vacuum (in a vacuum tube) or by ionized gas at low pressure (in a gas tube). Its operation depends on the generation and transfer of electrons through the tube from one electrode to another. The source of electrons is the cathode, usually a metallic electrode that releases a stream of electrons by one of several mechanisms described below. Once the electrons have been emitted, their movement is controlled by an electric field, a magnetic field, or both. An electric field is established by the application of a voltage between the electrodes in the tube, while a magnetic field may be produced outside the tube by an electromagnet or a permanent magnet. In its simplest form, an electron is attracted and accelerated by the positive electrode (a plate, or anode) and is repelled and slowed by the negative electrode (cathode). An electric field can be used to change the path of the electron stream, alter the number of flowing electrons (change the electric current), and modify their speed. The magnetic field serves primarily to control the movement of the electrons from one electrode to another.

Electron emission

In its most general sense, the emission of electrons results from directing energy in the form of heat, atomic-scale collisions, or strong electric fields to the cathode in such a way that electrons within the material are given enough kinetic energy to escape the surface. The most widely used mechanism in vacuum tubes is thermionic emission, or electron emission by application of heat.

The amount of energy needed to release electrons from a given material is known as its electronic work function. It follows that the ideal materials for cathodes are those that yield the lowest electronic work function. Barium, strontium, and thorium are commonly used for cathodes because of their low electronic work functions, from 1.2 to 3.5 electron volts (eV). Newer experimental materials, such as scandate (an alloy of barium and scandium oxide), have been discovered with slightly lower electronic work functions.

The anode, meanwhile, is usually made of a good conductor—such as iron, nickel, or carbon—that does not readily emit electrons at typical operating temperatures.

Thermionic emission

When solids are heated to high temperatures—about 1,000 °C (1,800 °F) or higher—electrons can be emitted from the surface. (This phenomenon was first observed by the American inventor Thomas Alva Edison in 1883 and is known as the Edison effect.) Thermionic emission is not thoroughly understood, but researchers have been able to describe it mathematically, using wave mechanics.

The most popular models rest on the Richardson-Dushman equation, derived in the 1920s, and the Langmuir-Child equation, formulated shortly thereafter. The former states that the current per unit of area, J, is given by

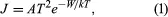
where k is Boltzman’s constant, A is a constant of the material and its surface finish and is theoretically about 120 amperes per square centimetre per kelvin, T is the temperature of the solid, and W is its work function.

As electrons are emitted by the application of heat, an electron cloud can form in front of the cathode. Such a cloud acts to repel low-energy electrons, which return to the cathode. This limiting mechanism is aptly referred to as the space-charge-limited operation. In a device such as the diode, the positive voltage applied to the anode attracts electrons from the cloud. The higher the voltage, the more electrons flow to the anode until the saturation voltage has been reached, at which point all the emitted electrons flow to the anode (known as the saturation current). In the space-charge-limited operation, the current density, J, is described by the Langmuir-Child law

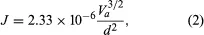
where V_a is the anode voltage and d is the distance between the anode and the cathode. The key characteristics of thermionic emission, as observed and predicted by equations (1) and (2), are the temperature-limited region and the space-charge-limited region. Much research has been concerned with the transition between the regions and with decreasing the work function of the cathode materials.

Secondary emission

When a metal or dielectric is bombarded by ions or electrons, electrons within the material may acquire sufficient kinetic energy to be emitted from the surface. The bombarding electrons are called primary, and the emitted electrons are designated secondary. The amount of secondary emission depends on the properties of the material and the energy and angle of incidence of the primary electrons. Material properties are characterized by the secondary-emission ratio, defined as the number of secondary electrons emitted per primary electron. Typically, the maximum secondary-emission ratio lies between 0.5 and 1.5 for pure metals and occurs for incident electron energies between 200 and 1,000 eV. The approximate energy distribution of secondary electrons emitted from a pure metal is skewed in such a way that about 85 percent of them have energies less than 20 eV.

Positive ion bombardment also can cause secondary emission, but it is much less efficient than electron bombardment, because only a small fraction of an ion’s energy can be imparted to (much lighter) electrons.

Field emission

Electron emission is influenced by an electric field applied at the cathode. For very strong electric fields, the electron emission becomes independent of temperature because the potential barrier at the surface of the cathode is made extremely narrow and electrons tunnel through the barrier even when they have low kinetic energy. Electric field strength must be about a billion volts per metre in order to cause field emissions.

Electron motion in a vacuum

Fundamental to all electron devices are the dynamics of charged particles under different electric and magnetic fields. The motion of an electron in a uniform field is given by a simple application of Isaac Newton’s second law of motion, force = mass × acceleration, in which the force is exerted on the electron by an applied electric field E (measured in volts per metre). Mathematically, the equation of motion of an electron in a uniform field is given by

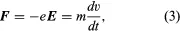
in which e is the electron charge 1.60 × 10⁻¹⁹ coulombs, E denotes the field in volts per metre, m is the electron mass 9.109 × 10⁻³¹ kilogram, and dv/dt denotes the rate of change of velocity, which is the electron’s acceleration.

If a magnetic field is also present, the electron will experience a second force, but only when the electron is in motion. The force will then be proportional to the product of charge and the velocity component that is perpendicular to the electric field E and to the magnetic flux density B (measured in webers per square centimetre). The force will be directed perpendicular to both the electric field and the electron velocity. Thus, an electron traveling parallel to an electric field and at right angles to a uniform magnetic field will be deflected in a direction perpendicular to both magnetic and electric fields. Because the force is constantly perpendicular to the velocity, the electron will trace out a perfectly circular trajectory and will maintain that motion at a rate called the cyclotron frequency, ω_c, given by e/mB. The circle traced out by the electron has a radius equal to mv/eB. This circular motion is exploited in many electron devices for generating or amplifying radio-frequency (RF) power.

An electron traveling parallel to a uniform magnetic field is unaffected by that field, but any departure from parallelism gives rise to a perpendicular component of velocity and thus a force. This force gives the nearly parallel electron a helical motion about the direction of the magnetic field, keeping it from diverging far from the parallel path. The equation of motion in any of these instances is

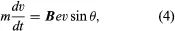
where v is the velocity of the electron in metres per second in the perpendicular direction to the plane of B and v, and θ is the angle between the directions of B and v. The magnetic flux density is expressed in webers per square centimetre (1 weber per centimetre² = 10⁴ gauss = 10⁷/4π amperes per metre).

Of interest, too, is the situation in which the magnetic and electric fields are perpendicular to each other. This configuration is used in beam-focusing devices as well as in a class of devices called magnetrons (see the section Magnetrons). In this case the motion of the electrons is a combination of translation and circular trajectories. The resultant trajectory is a cycloid.

Equations (3) and (4) are sufficient to solve for the path and time of transit of electrons in an electron tube except that they require E and B to be known, and these may depend on the presence of electrons or ions. The currents in electron tubes are small enough in most cases that their effect on the magnetic field is usually negligible. The cumulative effect of the electron or ion charge (called space charge) on the electric field cannot always be neglected, however, and this introduces computational difficulty unless the geometry is simple. Furthermore, the electrode currents are so dependent on space charges that the performance characteristics of electron tubes are largely determined by these charges. The electric field with or without space charge can be determined by Gauss’s theorem of electrostatics, which states how electric fields are associated with charges. Basically, the rate of change of E with distance is equal to ρ/ε₀, in which ρ is the electric charge density in coulombs per metre, and ε₀is the permittivity 8.85 × 10⁻¹² farads per metre.

The current per unit area, i, entering any surface—as that of an electrode in a tube—is the time rate of change of charge at that surface. This current is the sum of two components, one constituting the actual arrival of electrons at the electrode and the other resulting from the change of induced charge by any change of the electric field with time. Thus, i is the sum of ρv + ε₀dE/dt, where v is the electron density and dE/dt is the time-varying electric field. At low frequencies of operation or under steady conditions, the second term is not important. The contrary is true at high frequencies. This equation and the one relating the electric fields to the charges are fundamental to all high-vacuum electron tube phenomena and are sufficient to obtain theoretical solutions.

Energy transfer

The fundamental importance of a large class of electronic devices lies in their ability to amplify power. This power amplification results from the conversion of the energy stored in an external power supply to an output energy in the load circuit of the electron device. The mechanism that makes this conversion possible is the electron’s change in kinetic energy as it is accelerated or decelerated by an electric field. Because energy is conserved, the RF field will increase (amplification) if the electrons lose kinetic energy, and, conversely, it will decrease if the electrons gain kinetic energy.

When a modulated electron convection current flows in an electric field of the same modulation frequency, the power transfer, P, between the field and the electron is given by

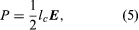
where l_c is the electron convection current and E is the electric field. Both l_c and E are complex quantities; substituting their values into equation (5) and separating the real and imaginary parts yields

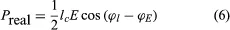
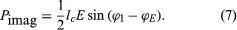
in which ϕ_l and ϕ_E are the phase angles of the modulated convection current and electric field, respectively. Insight into the meaning of equations (6) and (7) may be obtained by considering a physical picture. The negative electron flow (convection current) may be supposed to induce positive charges on the electrodes from which the E field emanates. If the phase is proper, meaning that the induced charges constructively add to the current associated with the modulated E field, the E field grows. Thus, in equations (6) and (7),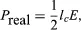andbecomes zero. Conversely, if the phases are 180° apart,goes to zero, and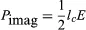and power is transferred from the field to the electron current. In practice, different methods are used to produce density modulation in an electron beam