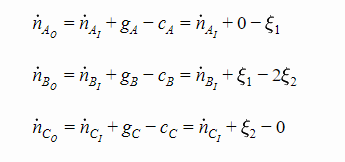Performing material balances on reactive systems is slightly more complex than for non-reactive systems
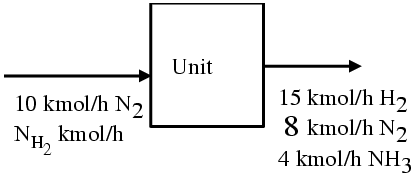
N2 + 3H2 -> 2NH3
While we can still do a balance on total mass, this is often not particularly useful (as we would like to know component compositions). What differs now is that a balance on total moles will not work (in general).
While the book notes three types of reactive balances, there are really only two types that are clearly distinct: a molecular species/extent of reaction balance; and a balance on atomic species.
For simplicity, this course will only focus on reactive processes that are open systems which are run at steady state. This yields a simplified balance equation of:
0=MI![]() −MO
−MO![]() +G−C
+G−C
Molecular/Extent of Reaction Balances
In this balance method we will examine each molecular species individually, and will typically rearrange our balance equation to be in the form:
MO![]() =MI
=MI![]() +G−C
+G−C
The G and C terms will then come directly from a combination of stoichiometry and the concept of the extent of reaction.
DEFINITION
The extent of reaction (![]() ) is a method of quantifying how many “times” a reaction has occurred. It has units of moles/time and numerically, it is chosen such that the stoichiometric coefficient times
) is a method of quantifying how many “times” a reaction has occurred. It has units of moles/time and numerically, it is chosen such that the stoichiometric coefficient times ![]() is equal to the quantity of species reacted.
is equal to the quantity of species reacted.
Using the above definition of the extent of reaction, it is a simple matter to write G and C in terms of this quantity simply using stoichiometry. In anticipation of performing reactive balances, we will switch to using molar quantities (n![]() ‘s rather than M
‘s rather than M![]() ‘s) so that we get:
‘s) so that we get:
nO![]() =nI
=nI![]() +g−c
+g−c
where we have used lowercase g and c to note molar quantities.
EXAMPLE
Let’s write the expressions for our figure above:
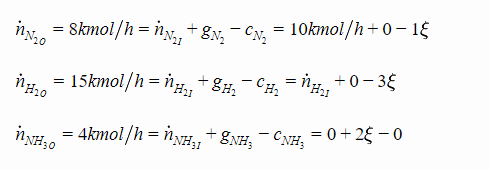
NOTE:
Typically “reactants” have g=0, while “products” have a zero initial concentration and have c=0. This obviously becomes more complex when multiple reactions take place.
Using the extent of reaction method for systems with multiple reactions involves including a new value of ![]() for each reaction, and then calculating c and g as the sum of applicable
for each reaction, and then calculating c and g as the sum of applicable ![]() ‘s.
‘s.
EXAMPLE
Consider the reaction network:
A -> B
2B -> C
If we assign ![]() 1 to the first reaction and
1 to the first reaction and ![]() 2 to the second, we get expressions that look like:
2 to the second, we get expressions that look like: