There exists an analogy between the diffusion of heat and electrical charge. Just as an electrical resistance is associated with the conduction of electricity, a thermal resistance may be associated with the conduction of heat. Defining resistance as the ratio of a driving potential to the corresponding transfer rate, it follows from Figure 3.4 that the thermal resistance for conduction is:

Series Circuits

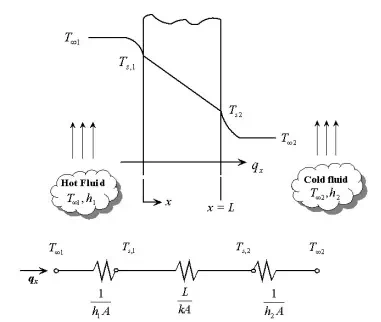
In the series circuits of heat transfer, heat is transferred in a series of stages that aren’t necessary of the same heat transfer mode. Figure 3.7 shows a plane wall subjected at its end to convective heat transfer. So in this case the heat is first transferred from the hot fluid to the wall surface by convection, then through the wall by conduction, and finally by convection from the second wall surface to the cold fluid. Here the heat quantity in each phase is the same so as current flowing in a series of electric resistances. Then from this analogy we may conclude that:

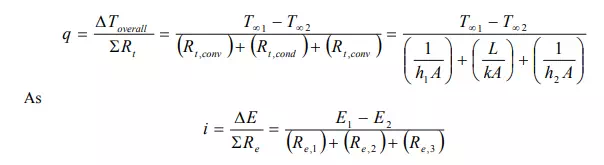
This thermal resistance analysis is very useful for more complex systems as composite walls and combined heat transfer modes. As examples examine Figure 3.8, if we use the analogy, the problem formulation will be much easier and less time consuming.