In the previous section the steady-state approximation was defined and illustrated. It was shown that this approximation is valid after a certain relaxation time that is a characteristic of the particular system under investigation. By perturbing the system and observing the recovery time, information concerning the kinetic parameters of the reaction sequence can be obtained. For example, with A B c, it was shown that the relaxation time when k]« k2 was ki I. Thus, relaxation methods can be very useful in determining the kinetic parameters of a particular sequence. Consider the simple case

and Ka can be calculated from the Gibbs functions of A and B, experimental determination of tr gives k] and L] via the use of Equations (4.3.2) and (4.3.3). Depending on the order of magnitude of t,., the experimentalist must choose an analytical technique that has a time constant for analysis smaller than tr

• For very fast reactions this can be a problem. A particularly useful method for determining relaxation times involves the use of flow reactors and labeled compounds. For example, say that the following reaction was proceeding over a solid catalyst:

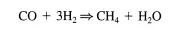
At steady-state conditions, l2CO can be replaced by 13CO while maintaining all other process parameters (e.g., temperature, flow rate) constant. The outlet from the reactor can be continuously monitored by mass spectroscopy. The decay of the concentration of 12CH4 and the increase in the concentration of 13CH4 can provide

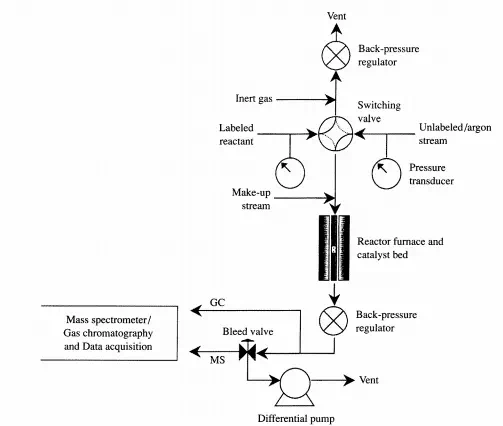
kinetic parameters for this system. This method is typically called “isotopic transient kinetic analysis.” Figure 4.3.la shows a schematic of an apparatus to perform the steady-state, isotopic transient kinetic analysis for the hydrogenolysis of ethane over a Ru/SiOz catalysis:

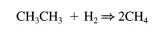
A sampling of the type of data obtained from this experiment is given in Figure 4.3.1b. Kinetic constants can be calculated from these data using analyses like those presented above for the simple reversible, first-order system.