A crystal lattice is made up of a very large number of unit cells where every lattice point is occupied by one constituent particle. The unit cell can be seen as a three dimension structure containing one or more atoms. We always observe some void spaces in the unit cell irrespective of the type of packing. Percentage of spaces filled by the particles in the unit cell is known as the packing fraction of the unit cell. In this section we shall learn about packing efficiency. Packing fraction of different types of packing in unit cells is calculated below:

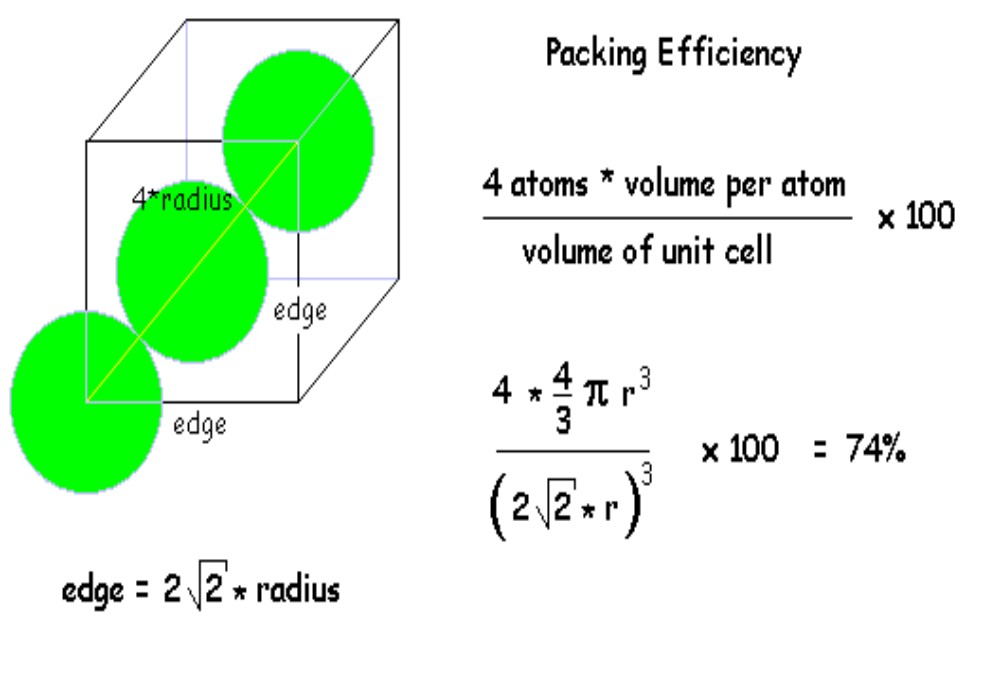
Packing efficiency in Hexagonal close packing and Cubic close packing structure:

Hexagonal close packing (hcp) and cubic close packing (ccp) have same packing efficiency. Let us take a unit cell of edge length “a”. Length of face diagonal, b can be calculated with the help of Pythagoras theorem,

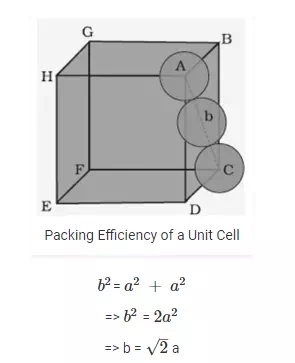
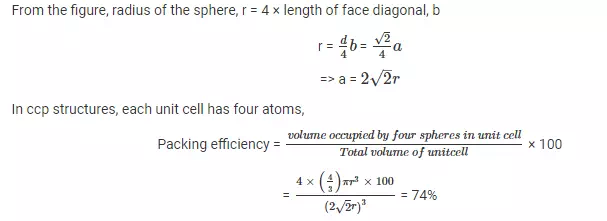
Packing efficiency in body centered cubic structure:

In body centered cubic unit cell, one atom is located at body center apart from corners of the cube. Let us take a unit cell of edge length “a”. Length of body diagonal, c can be calculated with help of Pythagoras theorem,