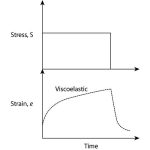
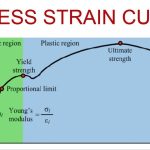
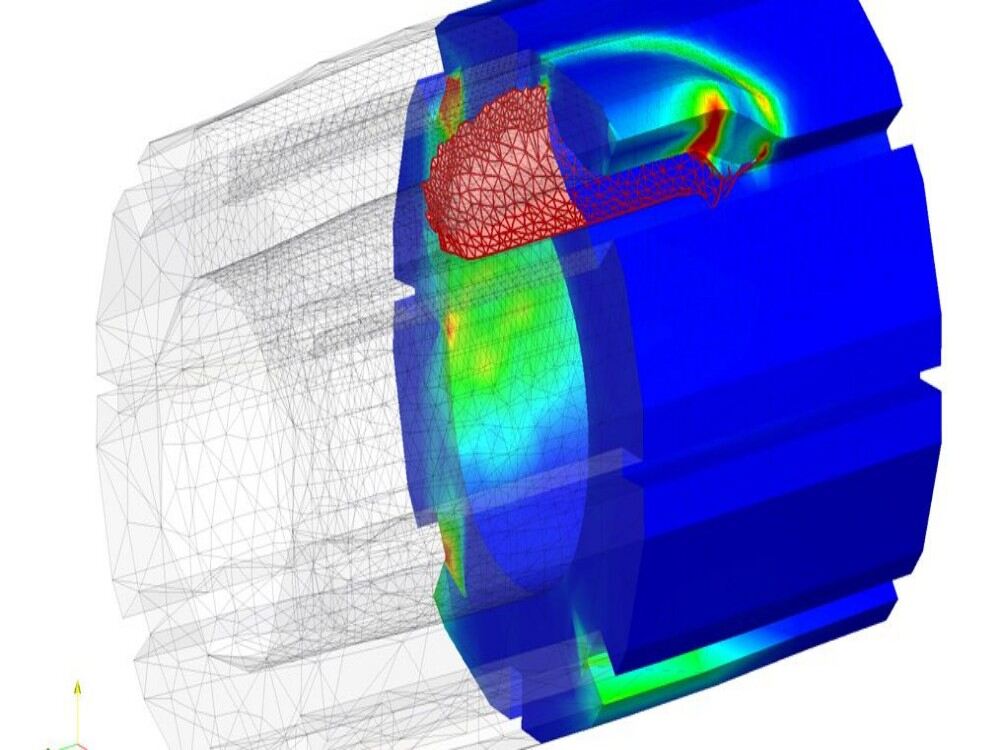
The digital computer revolutionized the practice of many areas of engineering and science, and solid mechanics was among the first fields to benefit from its impact. Many computational techniques have been used in this field, but the one that emerged by the end of 1970s as, by far, the most widely adopted is the finite-element method. This method was outlined by the mathematician Richard Courant in 1943 and was developed independently, and put to practical use on computers, in the mid-1950s by the aeronautical structures engineers M.J. Turner, Ray W. Clough, Harold Clifford Martin, and LeRoy J. Topp in the United States and J.H. Argyris and Sydney Kelsey in Britain. Their work grew out of earlier attempts at systematic structural analysis for complex frameworks of beam elements. The method was soon recast in a variational framework and related to earlier efforts at deriving approximate solutions of problems described by variational principles. The new technique involved substituting trial functions of unknown amplitude into the variational functional, which is then rendered stationary as an algebraic function of the amplitude coefficients. In the most common version of the finite-element method, the domain to be analyzed is divided into cells, or elements, and the displacement field within each element is interpolated in terms of displacements at a few points around the element boundary (and sometimes within it) called nodes. The interpolation is done so that the displacement field is continuous across element boundaries for any choice of the nodal displacements. The strain at every point can thus be expressed in terms of nodal displacements, and it is then required that the stresses associated with these strains, through the stress-strain relations of the material, satisfy the principle of virtual work for arbitrary variation of the nodal displacements. This generates as many simultaneous equations as there are degrees of freedom in the finite element model, and numerical techniques for solving such systems of equations are programmed for computer solution.
Posted inMechanics of Solids