The heat capacity of a substance is related to the question of how much energy does it take to raise the temperature of that substance by one unit. That would depend upon how much of the substance is being considered so the answer should be in terms of the amount of energy per standardized unit of the substance. The standardized unit could be a unit of mass but the standardized unit that makes comparison between different substances easiest is a mole; i.e., the amount containing Avogadro’s number (6.025×10²³) of molecules (or atoms as single unit molecules).

The heat capacity of a substance is defined in the reverse direction from what was referred to above. The heat capacity per unit substance, C, is the increase in internal energy of a substance U per unit increase in temperature T:

C = (∂U/∂T)

If the substance is a gas then it is important to specify whether the gas is being held at constant volume or constant pressure. For solids the difference is negligible.

A Classical Approach to Heat Capacity

A good deal of insight may be obtained from a very simple model of a solid. Consider the solid to be a three dimensional lattice of atoms in which the atoms are held near equilibrium positions by forces. If the force on an atom is proportional to its deviation from its equilibrium position then it is called a harmonic oscillator. For zero deviation the force is zero so the force for small deviations is proportional to the deviation. Thus any such solid can be considered to be composed of harmonic oscillators. In a cubic lattice the atoms can oscillate in three directions.

The average energy E of a harmonic oscillator in one dimension is kT, where k is Boltzmann’s constant. In three dimensions the average energy is 3kT. If there are N atoms in the lattice then the internal energy is U=N(3kT). Let A be Avogadro’s number (6.025×10²³). Then dividing and multiplying the equation of U by A gives

U = (N/A)(3AkT)
 

The ratio (N/A) is the number of moles of the substance, n, and Ak is denoted as R. Thus

U = n(3RT)
so
UM = (U/n) = 3RT
 

The heat capacity per unit mole of a substance at constant pressure is then defined as

Cp = (∂UM/∂T)
and thus from the above
Cp = 3R
 

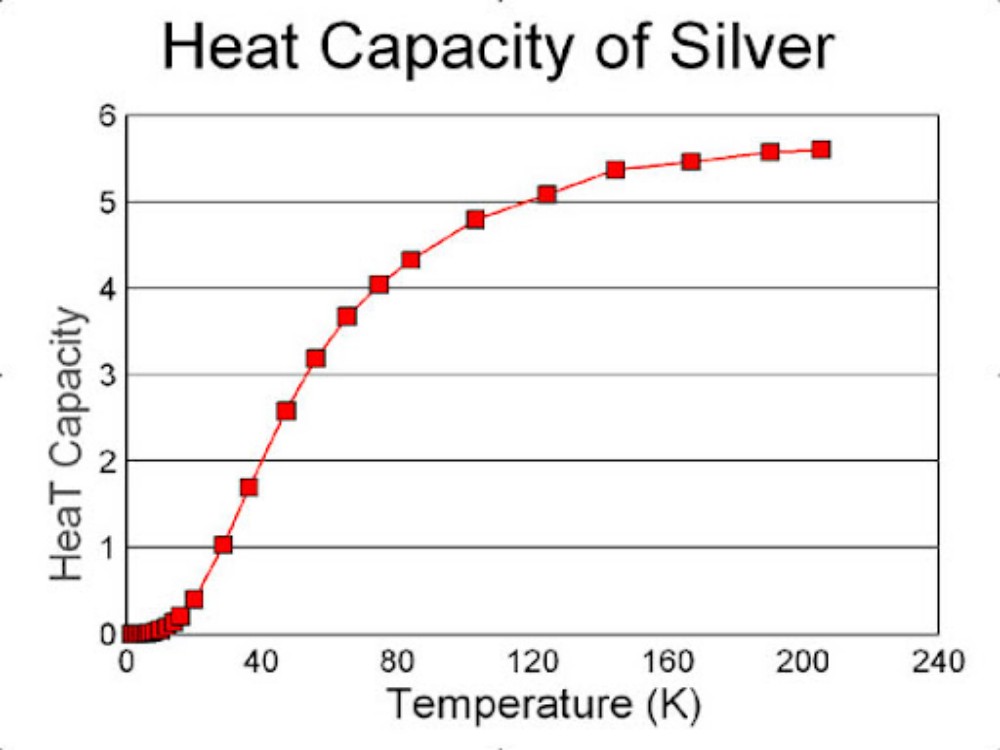
The value for C_p of 3R is about 6 calories per degree Kelvin. This is known as the Dulong and Petit value. It is a good approximation for the measured values for solids at room temperatures (300°K). At low temperatures the Dulong and Petit value is not a good approximation. Below is shown the heat capacity of metallic silver as a function of temperature.

The shape of the curve for T near zero is of interest. It appears to be proportional to a power of T, say T² or T³.