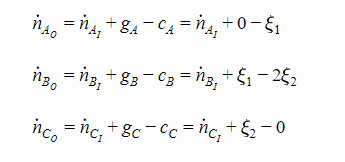Performing material balances on reactive systems is slightly more complex than for non-reactive systems

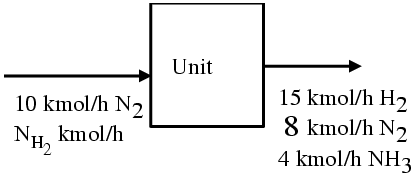
N2 + 3H2 -> 2NH3

While we can still do a balance on total mass, this is often not particularly useful (as we would like to know component compositions). What differs now is that a balance on total moles will not work (in general).

While the book notes three types of reactive balances, there are really only two types that are clearly distinct: a molecular species/extent of reaction balance; and a balance on atomic species.

For simplicity, this course will only focus on reactive processes that are open systems which are run at steady state. This yields a simplified balance equation of:

0=MI−MO+G−C

Molecular/Extent of Reaction Balances

In this balance method we will examine each molecular species individually, and will typically rearrange our balance equation to be in the form:

MO=MI+G−C

The G and C terms will then come directly from a combination of stoichiometry and the concept of the extent of reaction.

DEFINITION

The extent of reaction () is a method of quantifying how many “times” a reaction has occurred. It has units of moles/time and numerically, it is chosen such that the stoichiometric coefficient times  is equal to the quantity of species reacted.

Using the above definition of the extent of reaction, it is a simple matter to write G and C in terms of this quantity simply using stoichiometry. In anticipation of performing reactive balances, we will switch to using molar quantities (n‘s rather than M‘s) so that we get:

nO=nI+g−c

where we have used lowercase g and c to note molar quantities.

EXAMPLE

Let’s write the expressions for our figure above:

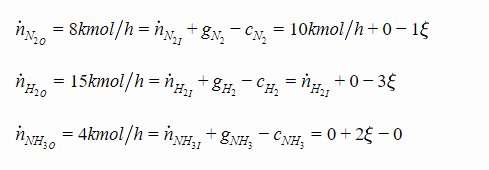
NOTE:

Typically “reactants” have g=0, while “products” have a zero initial concentration and have c=0. This obviously becomes more complex when multiple reactions take place.

Using the extent of reaction method for systems with multiple reactions involves including a new value of  for each reaction, and then calculating c and g as the sum of applicable ‘s.

EXAMPLE

Consider the reaction network:

A -> B
2B -> C

If we assign 1 to the first reaction and 2 to the second, we get expressions that look like: