Now that we have addressed units and dimensions and unit conversions, we can immediately make use of this information in a very practical and important application. A basic principle exists that equations must be dimensionally consistent. What the principle means is that each term in an equation must have the same net dimensions and units as every other term to which it is added or subtracted or equated. Consequently, dimensional considerations can be used to help identify the dimensions and units of terms or quantities in an equation. The concept of dimensional consistency can be illustrated by an equation that represents the pressure/volume/temperature behavior of a gas and is known as van der Waals’ equation, an equation to be discussed.
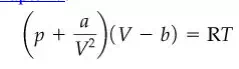
Inspection of the equation shows that the constant a must have the units of [(pressure)(volume) 2 ] because each term inside the first bracket must have units of pressure. If the units of pressure are atmospheres and those of volume are cubic centimeters, a will have the units specifically of [(atm) (cm) 6 ]. Similarly, b must have the same units as V, or in this particular case the units of cubic centimeters. If T is in kelvin, what must be the units of R? Check your answer by looking up R inside the front cover of the book. All equations must exhibit dimensional consistency.

Solution
After you inspect the equation that relates d as a function of t, you should be able to reach a decision about the units associated with each term on the right-hand side of the equation. Based on the concept of dimensional consistency, both values of 16.2 must have the associated units of microns (μm). The exponential term must be dimensionless so that 0.021 must have units of s –1 . To carry out the specified unit conversion for this equation, look up suitable conversion factors inside the front cover of this book (i.e., convert 16.2 μm to inches and 0.021 s –1 to min –1 ).

As you proceed with the study of chemical engineering, you will find that groups of symbols may be put together, either by theory or based on experiment, that have no net units. Such collections of variables or parameters are called dimensionless or nondimensional groups. One example is the Reynolds number that arises in fluid mechanics: