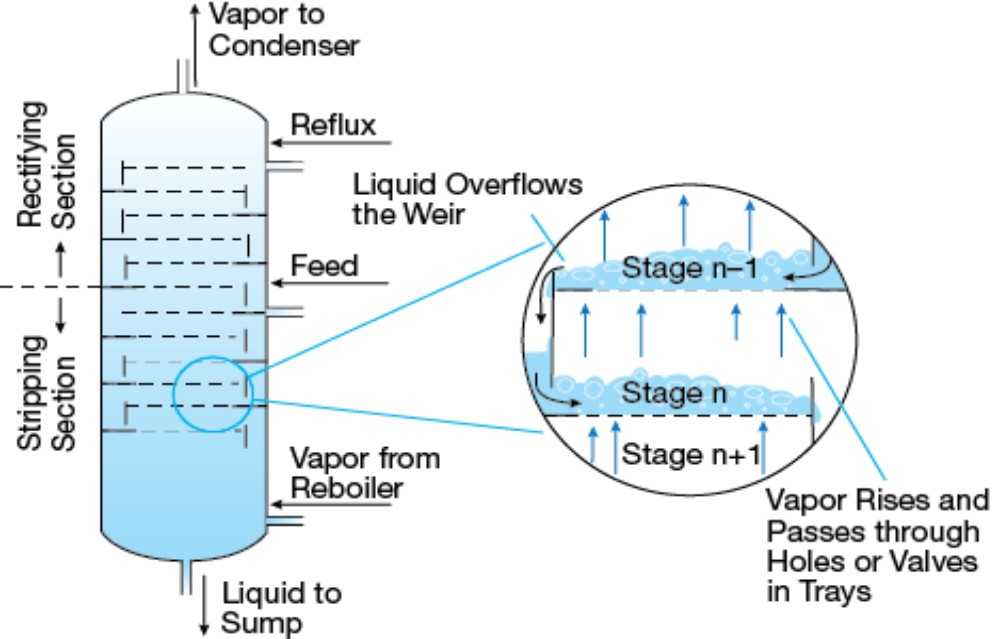
McCabeThiele Method McCabe and Thiele (1925) developed a graphical method to determine the theoretical number of stages required to effect the separation of a binary mixture (McCabe and Smith, 1976). This method uses the equilibrium curve diagram to determine the number of theoretical stages (trays) required to achieve a desired degree of separation. It assumes constant molar overflow and this implies that: (i) molal heats of vaporization of the components are roughly the same; (ii) heat effects are negligible. The information required for the systematic calculation are the VLE data, feed condition (temperature, composition), distillate and bottom compositions; and the reflux ratio, which is defined as the ratio of reflux liquid over the distillate product. For example, a column is to be designed for the separation of a binary mixture as shown in Figure 5.11.

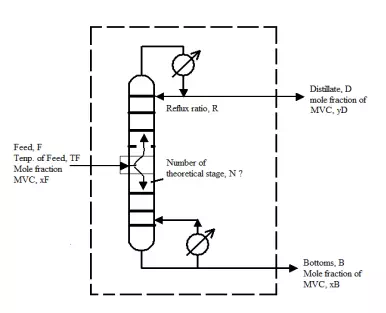
The feed has a concentration of xF (mole fraction) of the more volatile component, and a distillate having a concentration of xD of the more volatile component and a bottoms having a concentration of xB is desired. In its essence, the method involves the plotting on the equilibrium diagram three straight lines: the rectifying section operating line (ROL), the feed line (also known as the qline) and the stripping section operating line (SOL). An important parameter in the analysis of continuous distillation is the Reflux Ratio, defined as the quantity of liquid returned to the distillation column over the quantity of liquid withdrawn as product from the column, i.e. R = L / D. The reflux ratio R is important because the concentration of the more volatile component in the distillate (in mole fraction xD) can be changed by changing the value of R. The steps to be followed to determine the number of theoretical stages by McCabe-Thiele Method:

· Determination of the Rectifying section operating line (ROL).

· Determination the feed condition (q).

· Determination of the feed section operating line (q-line).

· Determination of required reflux ratio (R).

· Determination of the stripping section operating line (SOL).

Determination of the Rectifying section operating line (ROL)

Consider the rectifying section as shown in the Figure 5.12. Material balance can be written around the envelope shown in Figure 5.12:

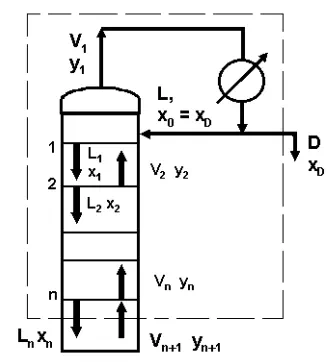
The Equation (5.18) is the rectifying section operating line (ROL) Equation having slope R/(R+1) and intercept, xD/(R+1) as shown in Figure 5.13. If xn = xD, then yn+1 = xD, the operating line passed through the point (xD, xD) on the 45o diagonal line. When the reflux ratio R changed, the ROL will change. Generally the rectifying operating line is expressed without subscript of n or n+1. Without subscript the ROL is expresses as: