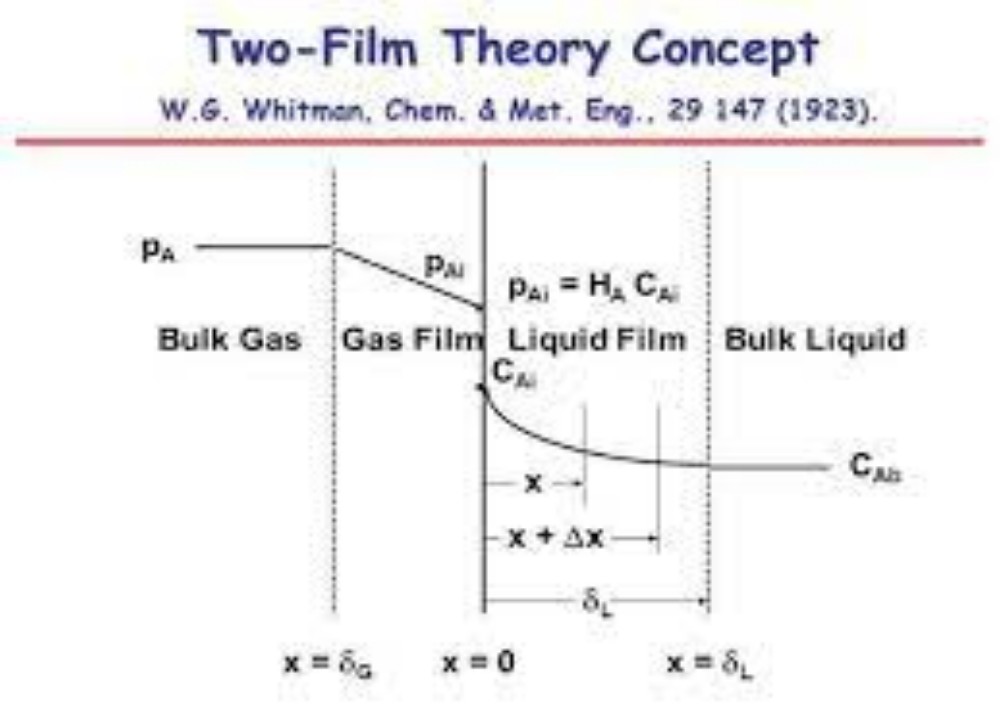
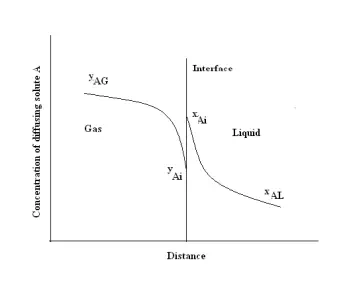
Consider the mass transfer of a solute A from the bulk of a gas phase to the bulk of a liquid phase. This can be shown graphically in terms of distance through the phases as shown in Figure 3.6. The concentration of A in the main body of the gas is yAG mole fraction and it falls to yAi at the interface. In the liquid, the concentration falls from xAi at the interface to xAL in the bulk liquid. According to Lews and Whitman (1924), there is no resistance to solute transfer across the interface separating the phases. Only diffusional resistances are residing in the fluids. The equilibrium concentrations yAi and xAi are obtained from the system’s equilibrium distribution curve.
This concept has been called the “two-resistance theory”. In the figure the concentration rise at the interface from yAi to xAi is not a barrier to diffusion in the direction gas to liquid. They are equilibrium concentrations. For steady state mass transfer, the rate at which A reaches the interface from the gas must be equal to the rate at which it diffuses to the bulk liquid, so that no accumulation or depletion of A at the interface occurs. Therefore the mass transfer flux of A in terms of mass transfer film coefficient for each phase can be written as:

Overall mass transfer coefficients Experimentally the mass transfer film coefficients ky and kx are difficult to measure except for cases where the concentration difference across one phase is small and can be neglected. Under these circumstances, the overall mass transfer coefficients Ky and Kx are measured on the basis of the gas phase or the liquid phase. The entire two-phase mass transfer effect can then be measured in terms of gas phase molar fraction driving force as:

where, Ky is based on the overall driving force for the gas phase, in mole/m2 .s and * A y is the value of concentration in the gas phase that would be in the equilibrium with xAL. Similarly, the entire two-phase mass transfer effect can then be measured in terms of liquid phase molar fraction driving force as:

where Kx is based on the overall driving force for the liquid phase, in mole/m2 .s and * A x is the value of concentration in the liquid phase that would be in the equilibrium with yAG. A relation between the overall coefficients and the individual mass transfer film coefficients can be obtained when the equilibrium relation is linear as Ai mxAi y = . The linear equilibrium condition can be obtained at the low concentrations, where Henry’s law is applicable. Here the proportionality constant m is defined as m= H/P. Utilizing the relationship, Ai mxAi y = , gas and liquid phase concentrations can be related by

The substitution of Equation (3.76) into the Equation (3.82) relates overall gas phase mass transfer coefficient (Ky) to the individual film coefficients by

The following relationships between the mass transfer resistances can be made from the Equations (3.83) and (3.85):
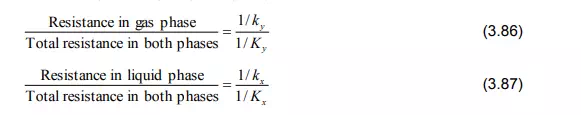
If solute A is very soluble in the liquid, m is very small. Then the term m/kx in Equation (3.83) becomes minor and consequently the major resistance is represented by 1/ky. In this case, it is said that the rate of mass transfer is gas phase controlled. In the extreme it becomes:

The total resistance equals the gas film resistance. The absorption of a very soluble gas, such as ammonia in water is an example of this kind. Conversely when solute A is relatively insoluble in the liquid, m is very large. Consequently the first term of Equation (3.85) becomes minor and the major resistance to the mass transfer resides within the liquid. The system becomes liquid film controlling. Finally this becomes:

The total resistance equals the liquid film resistance. The absorption of a gas of low solubility, such as carbon dioxide or oxygen in water is of this type of system.